Question Number 26981 by Tinkutara last updated on 31/Dec/17
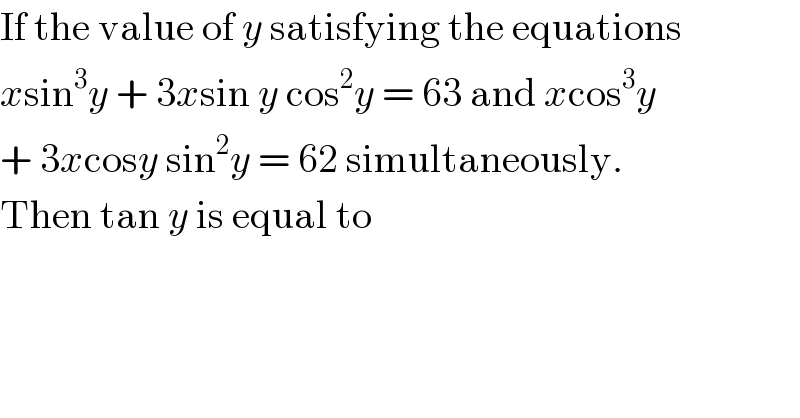
$$\mathrm{If}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{y}\:\mathrm{satisfying}\:\mathrm{the}\:\mathrm{equations} \\ $$$${x}\mathrm{sin}^{\mathrm{3}} {y}\:+\:\mathrm{3}{x}\mathrm{sin}\:{y}\:\mathrm{cos}^{\mathrm{2}} {y}\:=\:\mathrm{63}\:\mathrm{and}\:{x}\mathrm{cos}^{\mathrm{3}} {y} \\ $$$$+\:\mathrm{3}{x}\mathrm{cos}{y}\:\mathrm{sin}^{\mathrm{2}} {y}\:=\:\mathrm{62}\:\mathrm{simultaneously}. \\ $$$$\mathrm{Then}\:\mathrm{tan}\:{y}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to} \\ $$
Answered by ajfour last updated on 31/Dec/17
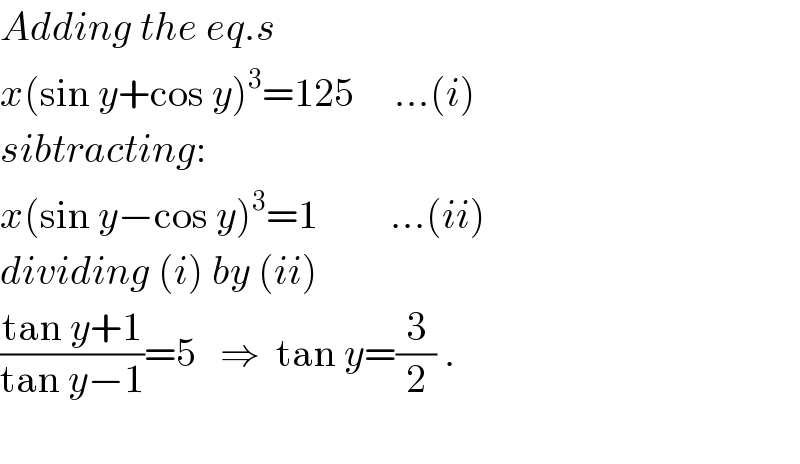
$${Adding}\:{the}\:{eq}.{s} \\ $$$${x}\left(\mathrm{sin}\:{y}+\mathrm{cos}\:{y}\right)^{\mathrm{3}} =\mathrm{125}\:\:\:\:\:…\left({i}\right) \\ $$$${sibtracting}: \\ $$$${x}\left(\mathrm{sin}\:{y}−\mathrm{cos}\:{y}\right)^{\mathrm{3}} =\mathrm{1}\:\:\:\:\:\:\:\:\:…\left({ii}\right) \\ $$$${dividing}\:\left({i}\right)\:{by}\:\left({ii}\right) \\ $$$$\frac{\mathrm{tan}\:{y}+\mathrm{1}}{\mathrm{tan}\:{y}−\mathrm{1}}=\mathrm{5}\:\:\:\Rightarrow\:\:\mathrm{tan}\:{y}=\frac{\mathrm{3}}{\mathrm{2}}\:. \\ $$$$ \\ $$
Commented by Tinkutara last updated on 01/Jan/18
Thank you very much Sir! I got the answer.
