Question Number 168585 by mkam last updated on 13/Apr/22
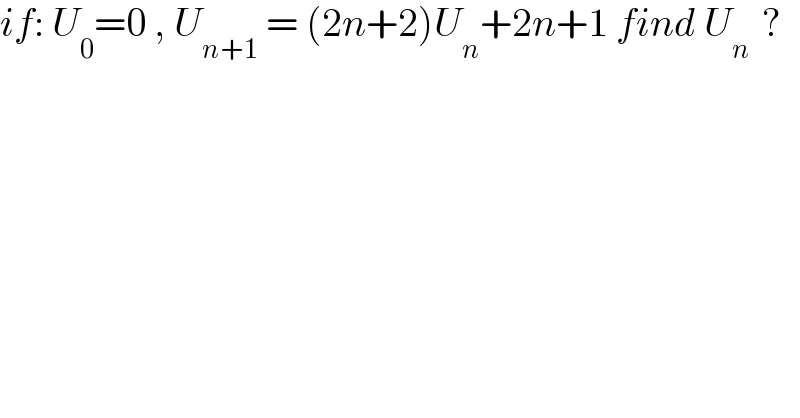
$${if}:\:{U}_{\mathrm{0}} =\mathrm{0}\:,\:{U}_{{n}+\mathrm{1}} \:=\:\left(\mathrm{2}{n}+\mathrm{2}\right){U}_{{n}} +\mathrm{2}{n}+\mathrm{1}\:{find}\:{U}_{{n}\:} \:? \\ $$
Commented by mr W last updated on 13/Apr/22

$${U}_{{n}} =\mathrm{2}^{{n}} {n}!−\mathrm{1} \\ $$
Commented by mkam last updated on 13/Apr/22
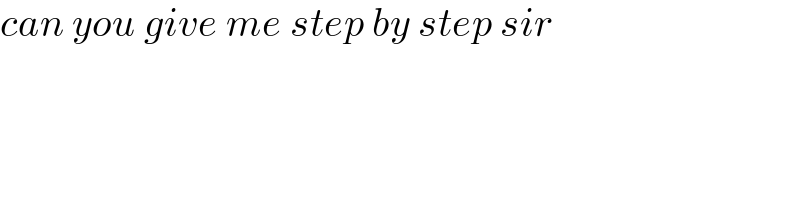
$${can}\:{you}\:{give}\:{me}\:{step}\:{by}\:{step}\:{sir} \\ $$
Answered by mr W last updated on 13/Apr/22
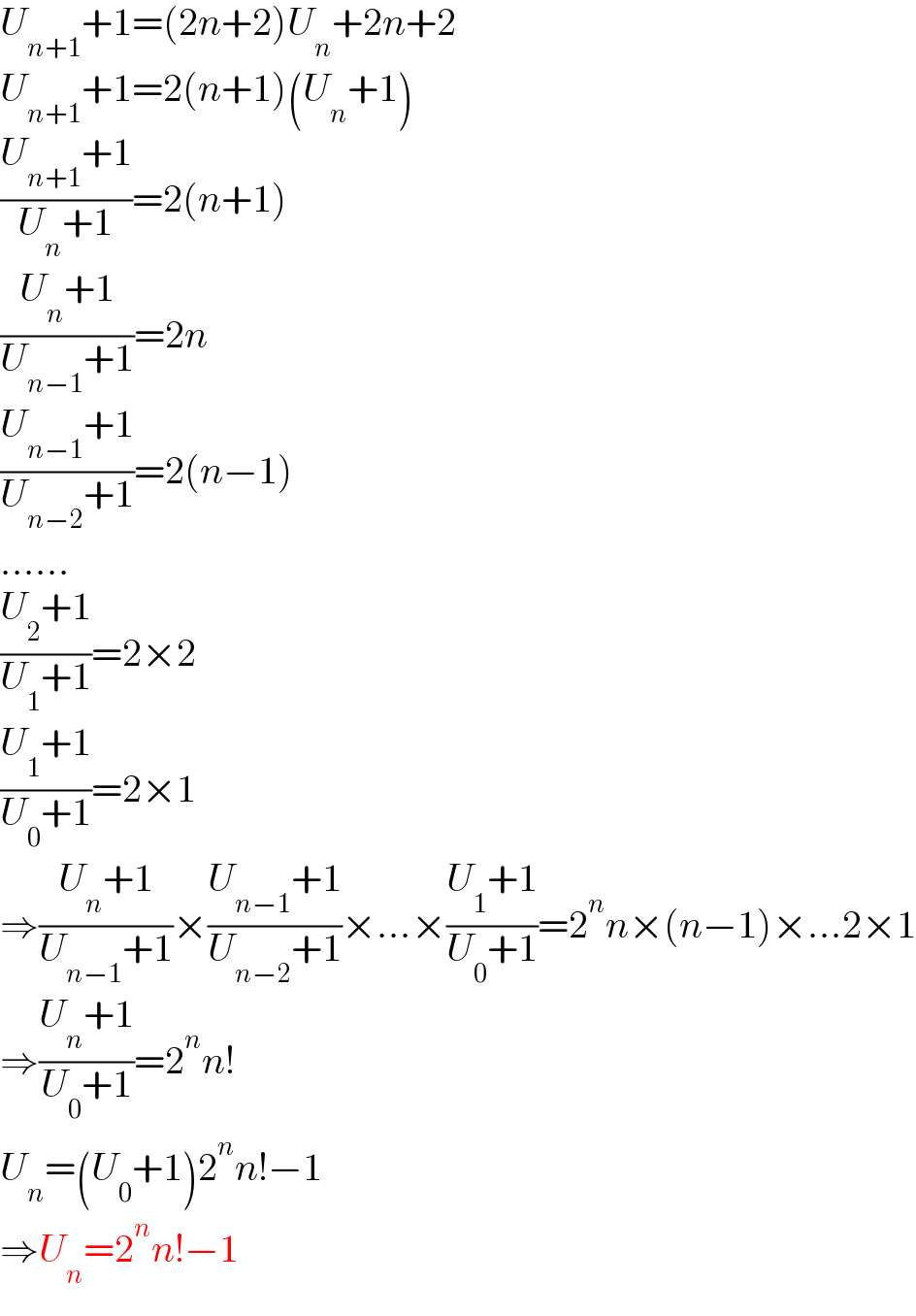
$${U}_{{n}+\mathrm{1}} +\mathrm{1}=\left(\mathrm{2}{n}+\mathrm{2}\right){U}_{{n}} +\mathrm{2}{n}+\mathrm{2} \\ $$$${U}_{{n}+\mathrm{1}} +\mathrm{1}=\mathrm{2}\left({n}+\mathrm{1}\right)\left({U}_{{n}} +\mathrm{1}\right) \\ $$$$\frac{{U}_{{n}+\mathrm{1}} +\mathrm{1}}{{U}_{{n}} +\mathrm{1}}=\mathrm{2}\left({n}+\mathrm{1}\right) \\ $$$$\frac{{U}_{{n}} +\mathrm{1}}{{U}_{{n}−\mathrm{1}} +\mathrm{1}}=\mathrm{2}{n} \\ $$$$\frac{{U}_{{n}−\mathrm{1}} +\mathrm{1}}{{U}_{{n}−\mathrm{2}} +\mathrm{1}}=\mathrm{2}\left({n}−\mathrm{1}\right) \\ $$$$…… \\ $$$$\frac{{U}_{\mathrm{2}} +\mathrm{1}}{{U}_{\mathrm{1}} +\mathrm{1}}=\mathrm{2}×\mathrm{2} \\ $$$$\frac{{U}_{\mathrm{1}} +\mathrm{1}}{{U}_{\mathrm{0}} +\mathrm{1}}=\mathrm{2}×\mathrm{1} \\ $$$$\Rightarrow\frac{{U}_{{n}} +\mathrm{1}}{{U}_{{n}−\mathrm{1}} +\mathrm{1}}×\frac{{U}_{{n}−\mathrm{1}} +\mathrm{1}}{{U}_{{n}−\mathrm{2}} +\mathrm{1}}×…×\frac{{U}_{\mathrm{1}} +\mathrm{1}}{{U}_{\mathrm{0}} +\mathrm{1}}=\mathrm{2}^{{n}} {n}×\left({n}−\mathrm{1}\right)×…\mathrm{2}×\mathrm{1} \\ $$$$\Rightarrow\frac{{U}_{{n}} +\mathrm{1}}{{U}_{\mathrm{0}} +\mathrm{1}}=\mathrm{2}^{{n}} {n}! \\ $$$${U}_{{n}} =\left({U}_{\mathrm{0}} +\mathrm{1}\right)\mathrm{2}^{{n}} {n}!−\mathrm{1} \\ $$$$\Rightarrow{U}_{{n}} =\mathrm{2}^{{n}} {n}!−\mathrm{1} \\ $$
