Question Number 83406 by jagoll last updated on 02/Mar/20
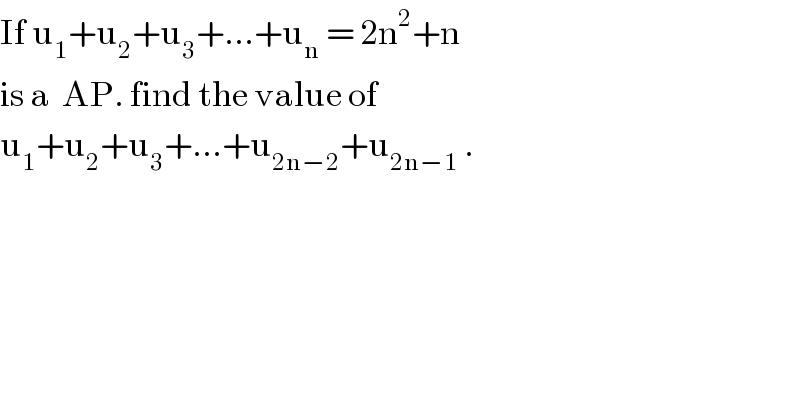
$$\mathrm{If}\:\mathrm{u}_{\mathrm{1}} +\mathrm{u}_{\mathrm{2}} +\mathrm{u}_{\mathrm{3}} +…+\mathrm{u}_{\mathrm{n}} \:=\:\mathrm{2n}^{\mathrm{2}} +\mathrm{n}\: \\ $$$$\mathrm{is}\:\mathrm{a}\:\:\mathrm{AP}.\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\: \\ $$$$\mathrm{u}_{\mathrm{1}} +\mathrm{u}_{\mathrm{2}} +\mathrm{u}_{\mathrm{3}} +…+\mathrm{u}_{\mathrm{2n}−\mathrm{2}} +\mathrm{u}_{\mathrm{2n}−\mathrm{1}} \:. \\ $$
Commented by jagoll last updated on 03/Mar/20

$$\mathrm{my}\:\mathrm{way}\: \\ $$$$\mathrm{from}\:\mathrm{s}_{\mathrm{n}} \:=\:\mathrm{2n}^{\mathrm{2}} +\mathrm{n}\:\begin{cases}{\mathrm{u}_{\mathrm{1}} =\mathrm{3}}\\{\mathrm{u}_{\mathrm{n}} \:=\:\mathrm{4n}−\mathrm{1}}\end{cases} \\ $$$$\mathrm{u}_{\mathrm{1}} +\mathrm{u}_{\mathrm{2}} +\mathrm{u}_{\mathrm{3}} +…+\mathrm{u}_{\mathrm{2n}−\mathrm{2}} +\mathrm{u}_{\mathrm{2n}−\mathrm{1}} \:=\:\mathrm{M} \\ $$$$\mathrm{let}\:\mathrm{2n}−\mathrm{1}\:=\:\mathrm{k}\: \\ $$$$\mathrm{M}\:=\:\frac{\mathrm{k}}{\mathrm{2}}\left(\mathrm{3}+\mathrm{u}_{\mathrm{k}} \right)=\frac{\mathrm{k}}{\mathrm{2}}\left(\mathrm{3}+\mathrm{4k}−\mathrm{1}\right) \\ $$$$\mathrm{M}\:=\:\frac{\mathrm{k}}{\mathrm{2}}\left(\mathrm{4k}+\mathrm{2}\right)\:=\:\mathrm{k}\:\left(\mathrm{2k}+\mathrm{1}\right) \\ $$$$\mathrm{M}\:=\:\left(\mathrm{2n}−\mathrm{1}\right)\left(\mathrm{4k}−\mathrm{1}\right)\:=\:\mathrm{8n}^{\mathrm{2}} −\mathrm{6n}+\mathrm{1} \\ $$$$ \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 02/Mar/20

$${we}\:{have}\:{u}_{\mathrm{1}} +{u}_{\mathrm{2}} +….+{u}_{{n}} =\mathrm{2}{n}^{\mathrm{2}} \:+{n} \\ $$$${u}_{\mathrm{1}} +{u}_{\mathrm{2}} +….+{u}_{{n}} +{u}_{{n}+\mathrm{1}} =\mathrm{2}\left({n}+\mathrm{1}\right)^{\mathrm{2}} \:+{n}+\mathrm{1}\:\Rightarrow \\ $$$${u}_{{n}+\mathrm{1}} =\mathrm{2}\left({n}+\mathrm{1}\right)^{\mathrm{2}} \:+{n}+\mathrm{1}−\mathrm{2}{n}^{\mathrm{2}} −{n}\:=\mathrm{2}\left({n}^{\mathrm{2}} \:+\mathrm{2}{n}+\mathrm{1}\right)−\mathrm{2}{n}^{\mathrm{2}} +\mathrm{1} \\ $$$$=\mathrm{2}{n}^{\mathrm{2}} +\mathrm{4}{n}+\mathrm{2}−\mathrm{2}{n}^{\mathrm{2}} \:+\mathrm{1}\:=\mathrm{4}{n}+\mathrm{3}\:\Rightarrow{u}_{{n}} =\mathrm{4}\left({n}−\mathrm{1}\right)+\mathrm{3}\:=\mathrm{4}{n}−\mathrm{1}\:\Rightarrow \\ $$$${u}_{\mathrm{1}} +{u}_{\mathrm{2}} +….+{u}_{\mathrm{2}{n}−\mathrm{1}} =\frac{\mathrm{2}{n}−\mathrm{1}−\mathrm{1}+\mathrm{1}}{\mathrm{2}}\left({u}_{\mathrm{1}} +{u}_{\mathrm{2}{n}−\mathrm{1}} \right) \\ $$$$=\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}}\left\{\mathrm{3}\:+\mathrm{4}\left(\mathrm{2}{n}−\mathrm{1}\right)−\mathrm{1}\right\}\:=\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}+\mathrm{8}{n}−\mathrm{4}\right) \\ $$$$=\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{4}{n}−\mathrm{1}\right)=\mathrm{8}{n}^{\mathrm{2}} −\mathrm{2}{n}−\mathrm{4}{n}+\mathrm{1}\:=\mathrm{8}{n}^{\mathrm{2}} −\mathrm{6}{n}\:+\mathrm{1} \\ $$
Commented by mathmax by abdo last updated on 02/Mar/20

$${u}_{{n}} =\mathrm{4}{n}−\mathrm{1} \\ $$
Answered by mind is power last updated on 02/Mar/20
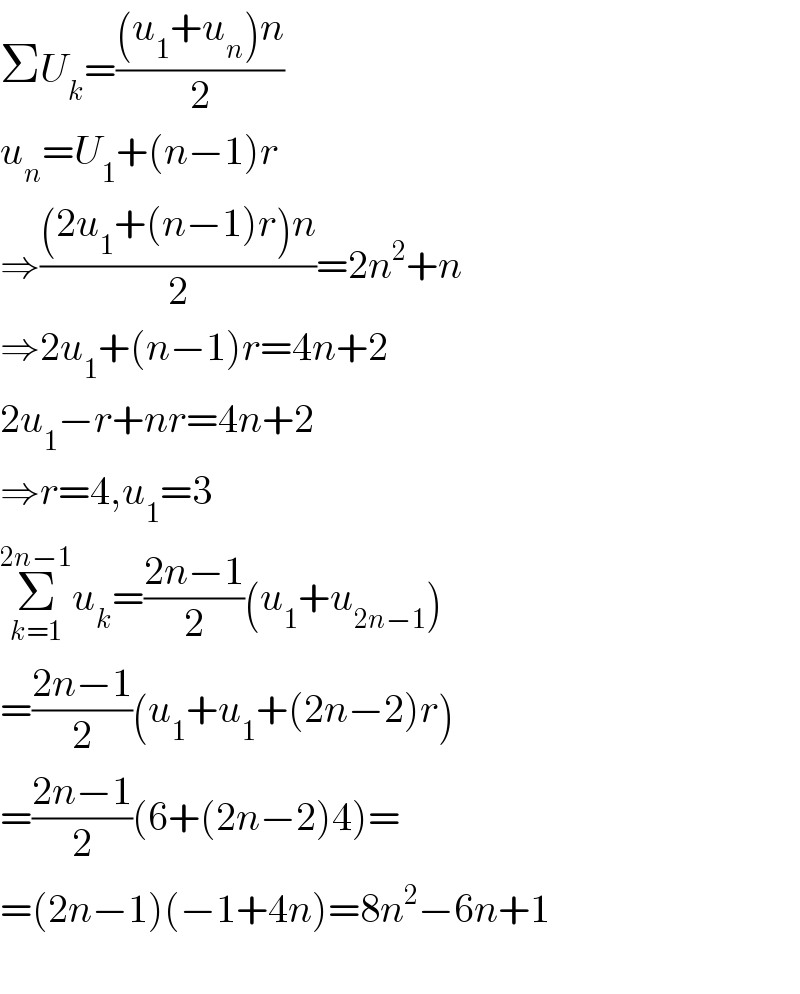
$$\Sigma{U}_{{k}} =\frac{\left({u}_{\mathrm{1}} +{u}_{{n}} \right){n}}{\mathrm{2}} \\ $$$${u}_{{n}} ={U}_{\mathrm{1}} +\left({n}−\mathrm{1}\right){r} \\ $$$$\Rightarrow\frac{\left(\mathrm{2}{u}_{\mathrm{1}} +\left({n}−\mathrm{1}\right){r}\right){n}}{\mathrm{2}}=\mathrm{2}{n}^{\mathrm{2}} +{n} \\ $$$$\Rightarrow\mathrm{2}{u}_{\mathrm{1}} +\left({n}−\mathrm{1}\right){r}=\mathrm{4}{n}+\mathrm{2} \\ $$$$\mathrm{2}{u}_{\mathrm{1}} −{r}+{nr}=\mathrm{4}{n}+\mathrm{2} \\ $$$$\Rightarrow{r}=\mathrm{4},{u}_{\mathrm{1}} =\mathrm{3} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{2}{n}−\mathrm{1}} {\sum}}{u}_{{k}} =\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}}\left({u}_{\mathrm{1}} +{u}_{\mathrm{2}{n}−\mathrm{1}} \right) \\ $$$$=\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}}\left({u}_{\mathrm{1}} +{u}_{\mathrm{1}} +\left(\mathrm{2}{n}−\mathrm{2}\right){r}\right) \\ $$$$=\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}}\left(\mathrm{6}+\left(\mathrm{2}{n}−\mathrm{2}\right)\mathrm{4}\right)= \\ $$$$=\left(\mathrm{2}{n}−\mathrm{1}\right)\left(−\mathrm{1}+\mathrm{4}{n}\right)=\mathrm{8}{n}^{\mathrm{2}} −\mathrm{6}{n}+\mathrm{1} \\ $$$$ \\ $$
Commented by mind is power last updated on 02/Mar/20

$$\mathrm{2}{n}−\mathrm{1}=\mathrm{11}\:{sir} \\ $$
Commented by jagoll last updated on 02/Mar/20
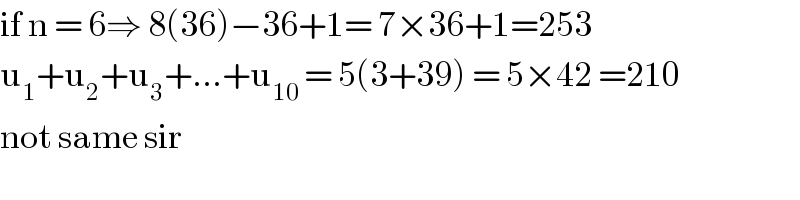
$$\mathrm{if}\:\mathrm{n}\:=\:\mathrm{6}\Rightarrow\:\mathrm{8}\left(\mathrm{36}\right)−\mathrm{36}+\mathrm{1}=\:\mathrm{7}×\mathrm{36}+\mathrm{1}=\mathrm{253} \\ $$$$\mathrm{u}_{\mathrm{1}} +\mathrm{u}_{\mathrm{2}} +\mathrm{u}_{\mathrm{3}} +…+\mathrm{u}_{\mathrm{10}\:} =\:\mathrm{5}\left(\mathrm{3}+\mathrm{39}\right)\:=\:\mathrm{5}×\mathrm{42}\:=\mathrm{210} \\ $$$$\mathrm{not}\:\mathrm{same}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 02/Mar/20

$${S}_{{n}} =\mathrm{2}{n}^{\mathrm{2}} +{n}={n}\left(\mathrm{2}{n}+\mathrm{1}\right) \\ $$$${S}_{\mathrm{2}{n}−\mathrm{1}} =\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}\left(\mathrm{2}{n}−\mathrm{1}\right)+\mathrm{1}\right)=\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{4}{n}−\mathrm{1}\right) \\ $$
Commented by mr W last updated on 02/Mar/20
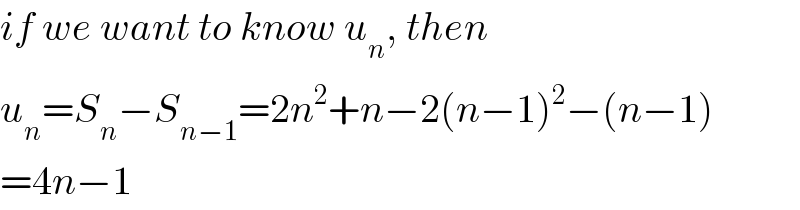
$${if}\:{we}\:{want}\:{to}\:{know}\:{u}_{{n}} ,\:{then} \\ $$$${u}_{{n}} ={S}_{{n}} −{S}_{{n}−\mathrm{1}} =\mathrm{2}{n}^{\mathrm{2}} +{n}−\mathrm{2}\left({n}−\mathrm{1}\right)^{\mathrm{2}} −\left({n}−\mathrm{1}\right) \\ $$$$=\mathrm{4}{n}−\mathrm{1} \\ $$
Answered by TANMAY PANACEA last updated on 02/Mar/20
![put n=1 u_1 =3 put n=2 u_1 +u_2 =10 so u_2 =7 n=3 u_1 +u_2 +u_3 =21 so u_3 =11 so first term ofA.P=3 common difference=4 S_(2n−1) =((2n−1)/2)[2×3+(2n−1−1)×4] =((2n−1)/2)×[6+8n−8] =(2n−1)(4n−1)](https://www.tinkutara.com/question/Q83465.png)
$${put}\:{n}=\mathrm{1}\:\:{u}_{\mathrm{1}} =\mathrm{3} \\ $$$${put}\:{n}=\mathrm{2}\:\:\:\:{u}_{\mathrm{1}} +{u}_{\mathrm{2}} =\mathrm{10}\:\:\boldsymbol{{so}}\:\boldsymbol{{u}}_{\mathrm{2}} =\mathrm{7} \\ $$$$\boldsymbol{{n}}=\mathrm{3}\:\:{u}_{\mathrm{1}} +{u}_{\mathrm{2}} +{u}_{\mathrm{3}} =\mathrm{21}\:\:\:{so}\:{u}_{\mathrm{3}} =\mathrm{11} \\ $$$${so}\:{first}\:{term}\:{of}\boldsymbol{{A}}.{P}=\mathrm{3} \\ $$$${common}\:{difference}=\mathrm{4} \\ $$$${S}_{\mathrm{2}{n}−\mathrm{1}} =\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}}\left[\mathrm{2}×\mathrm{3}+\left(\mathrm{2}{n}−\mathrm{1}−\mathrm{1}\right)×\mathrm{4}\right] \\ $$$$=\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}}×\left[\mathrm{6}+\mathrm{8}{n}−\mathrm{8}\right] \\ $$$$=\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{4}{n}−\mathrm{1}\right) \\ $$
