Question Number 78894 by gopikrishnan last updated on 21/Jan/20
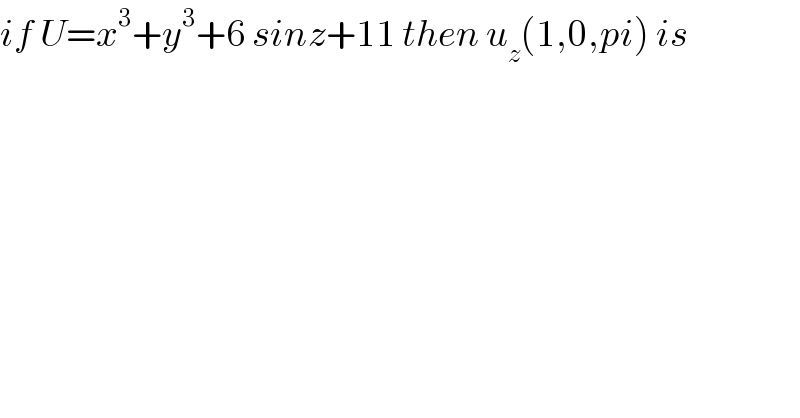
$${if}\:{U}={x}^{\mathrm{3}} +{y}^{\mathrm{3}} +\mathrm{6}\:{sinz}+\mathrm{11}\:{then}\:{u}_{{z}} \left(\mathrm{1},\mathrm{0},{pi}\right)\:{is} \\ $$
Commented by mathmax by abdo last updated on 22/Jan/20
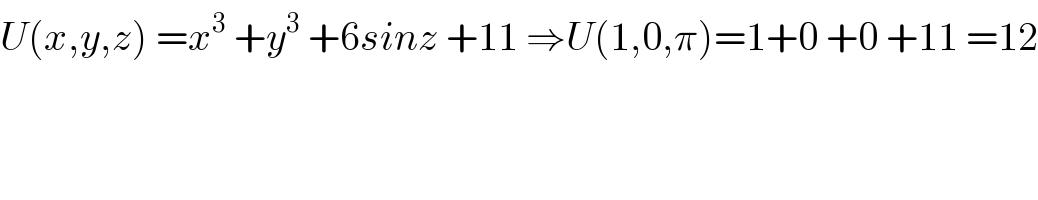
$${U}\left({x},{y},{z}\right)\:={x}^{\mathrm{3}} \:+{y}^{\mathrm{3}} \:+\mathrm{6}{sinz}\:+\mathrm{11}\:\Rightarrow{U}\left(\mathrm{1},\mathrm{0},\pi\right)=\mathrm{1}+\mathrm{0}\:+\mathrm{0}\:+\mathrm{11}\:=\mathrm{12} \\ $$
