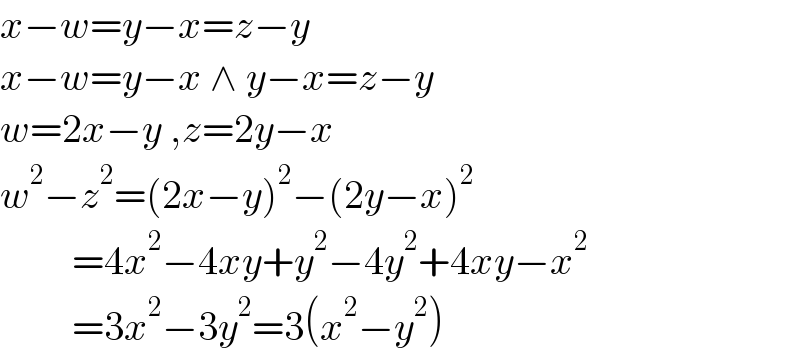If-w-x-y-and-z-be-four-consecutive-terms-of-any-AP-then-show-that-w-2-z-2-3-x-2-y-2-

Question Number 175839 by Rasheed.Sindhi last updated on 08/Sep/22

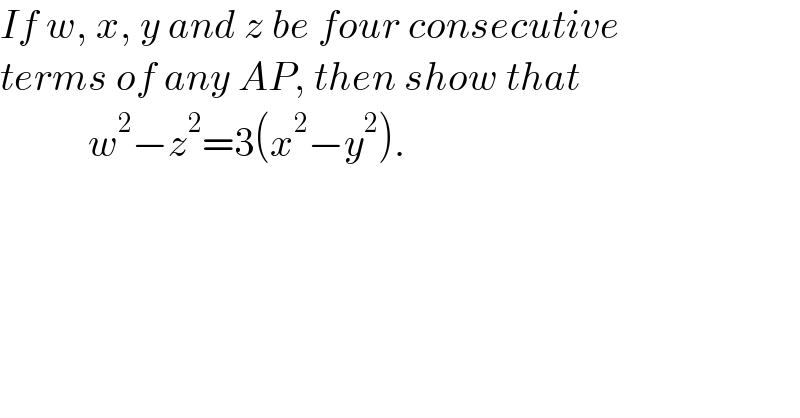
I f w, x, y a n d z b e f o u r c o n s e c u t i v e

t e r m s o f a n y A P, t h e n s h o w t h a t

w^{2} - z^{2} = 3 (x^{2} - y^{2}) .

Answered by mr W last updated on 08/Sep/22

l e t c = \frac{x + y}{2}, d = c o m m o n d i f f e r e n c e

w = c - \frac{3 d}{2}

x = c - \frac{d}{2}

y = c + \frac{d}{2}

z = c + \frac{3 d}{2}

w^{2} - z^{2} = {(c - \frac{3 d}{2})}^{2} - {(c + \frac{3 d}{2})}^{2} = - 6 c d

x^{2} - y^{2} = {(c - \frac{d}{2})}^{2} - {(c + \frac{d}{2})}^{2} = - 2 c d

\Rightarrow w^{2} - z^{2} = 3 (x^{2} - y^{2})

Commented by peter frank last updated on 08/Sep/22

thans

Commented by Rasheed.Sindhi last updated on 08/Sep/22

N ice sir, than k s!

Commented by Tawa11 last updated on 15/Sep/22

Great sir .

Answered by Rasheed.Sindhi last updated on 08/Sep/22

x - w = y - x = z - y

x - w = y - x \land y - x = z - y

w = 2 x - y, z = 2 y - x

w^{2} - z^{2} = {(2 x - y)}^{2} - {(2 y - x)}^{2}

= 4 x^{2} - 4 x y + y^{2} - 4 y^{2} + 4 x y - x^{2}

= 3 x^{2} - 3 y^{2} = 3 (x^{2} - y^{2})