Question Number 90485 by Maclaurin Stickker last updated on 23/Apr/20
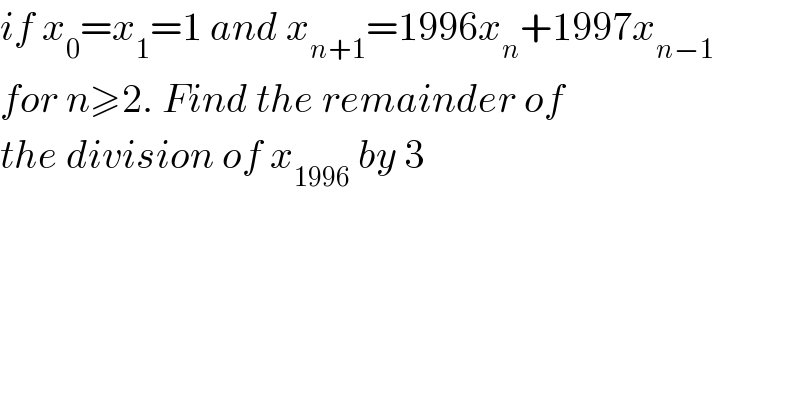
$${if}\:{x}_{\mathrm{0}} ={x}_{\mathrm{1}} =\mathrm{1}\:{and}\:{x}_{{n}+\mathrm{1}} =\mathrm{1996}{x}_{{n}} +\mathrm{1997}{x}_{{n}−\mathrm{1}} \\ $$$${for}\:{n}\geqslant\mathrm{2}.\:{Find}\:{the}\:{remainder}\:{of} \\ $$$${the}\:{division}\:{of}\:{x}_{\mathrm{1996}} \:{by}\:\mathrm{3} \\ $$
Commented by Maclaurin Stickker last updated on 23/Apr/20

$${I}\:{find}\:{the}\:{general}\:{term}\:{of}\:{sequence} \\ $$$${x}_{{n}} =\frac{\mathrm{998}\left(−\mathrm{1}\right)^{{n}} +\mathrm{1997}^{{n}} }{\mathrm{999}} \\ $$$${If}\:{it}\:{is}\:{right},\:{how}\:{could}\:{I}\:{find}\:{the}\:{remainder} \\ $$$${without}\:{Newton}'{s}\:{Binomial}? \\ $$
