Question Number 130580 by bramlexs22 last updated on 27/Jan/21
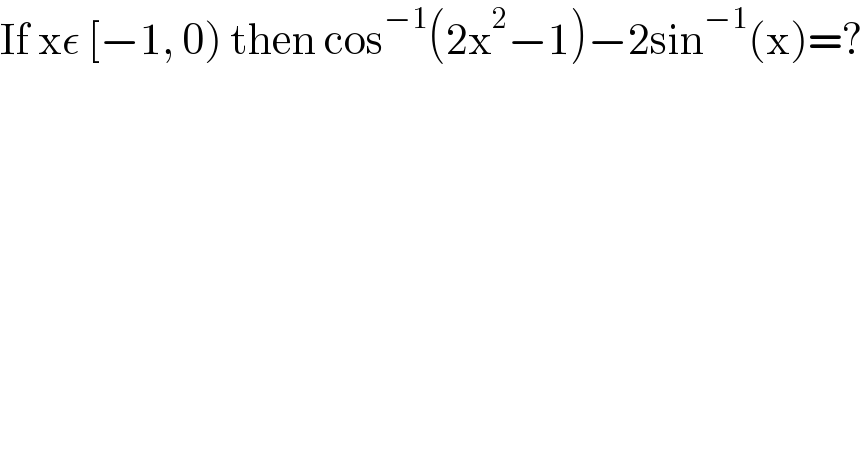
$$\mathrm{If}\:\mathrm{x}\epsilon\:\left[−\mathrm{1},\:\mathrm{0}\right)\:\mathrm{then}\:\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{2x}^{\mathrm{2}} −\mathrm{1}\right)−\mathrm{2sin}^{−\mathrm{1}} \left(\mathrm{x}\right)=? \\ $$
Commented by EDWIN88 last updated on 27/Jan/21

$$\pi \\ $$
Answered by mindispower last updated on 27/Jan/21
![x=cos((θ/2)),θ∈[π,2π[ ⇒cos^− (2cos^2 ((θ/2))−1)−2sin^− (cos((θ/2))) =cos^− (cos(θ))−2sin^− (sin(((π−θ)/2))) sin^− (sin(((π−θ)/2)))=((π−θ)/2),((π−θ)/2)∈]−(π/2),0[ cos^− (cos(θ))=cos^− (cos(2π−θ))=2π−θ 2π−θ−2(((π−θ)/2))=π](https://www.tinkutara.com/question/Q130611.png)
$${x}={cos}\left(\frac{\theta}{\mathrm{2}}\right),\theta\in\left[\pi,\mathrm{2}\pi\left[\right.\right. \\ $$$$\Rightarrow{cos}^{−} \left(\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)−\mathrm{1}\right)−\mathrm{2}{sin}^{−} \left({cos}\left(\frac{\theta}{\mathrm{2}}\right)\right) \\ $$$$={cos}^{−} \left({cos}\left(\theta\right)\right)−\mathrm{2}{sin}^{−} \left({sin}\left(\frac{\pi−\theta}{\mathrm{2}}\right)\right) \\ $$$$\left.{sin}^{−} \left({sin}\left(\frac{\pi−\theta}{\mathrm{2}}\right)\right)=\frac{\pi−\theta}{\mathrm{2}},\frac{\pi−\theta}{\mathrm{2}}\in\right]−\frac{\pi}{\mathrm{2}},\mathrm{0}\left[\right. \\ $$$${cos}^{−} \left({cos}\left(\theta\right)\right)={cos}^{−} \left({cos}\left(\mathrm{2}\pi−\theta\right)\right)=\mathrm{2}\pi−\theta \\ $$$$\mathrm{2}\pi−\theta−\mathrm{2}\left(\frac{\pi−\theta}{\mathrm{2}}\right)=\pi \\ $$$$ \\ $$
