Question Number 111534 by Aina Samuel Temidayo last updated on 04/Sep/20
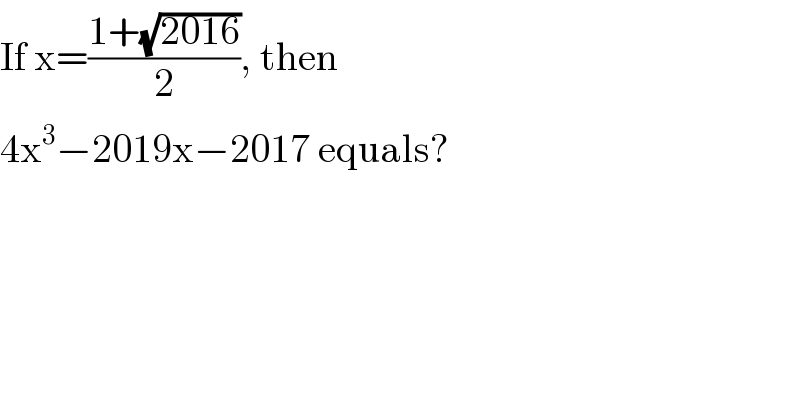
$$\mathrm{If}\:\mathrm{x}=\frac{\mathrm{1}+\sqrt{\mathrm{2016}}}{\mathrm{2}},\:\mathrm{then} \\ $$$$\mathrm{4x}^{\mathrm{3}} −\mathrm{2019x}−\mathrm{2017}\:\mathrm{equals}? \\ $$
Answered by Lordose last updated on 04/Sep/20

$$ \\ $$$$\bigstar\:\:\:−\mathrm{2} \\ $$
Answered by 1549442205PVT last updated on 04/Sep/20
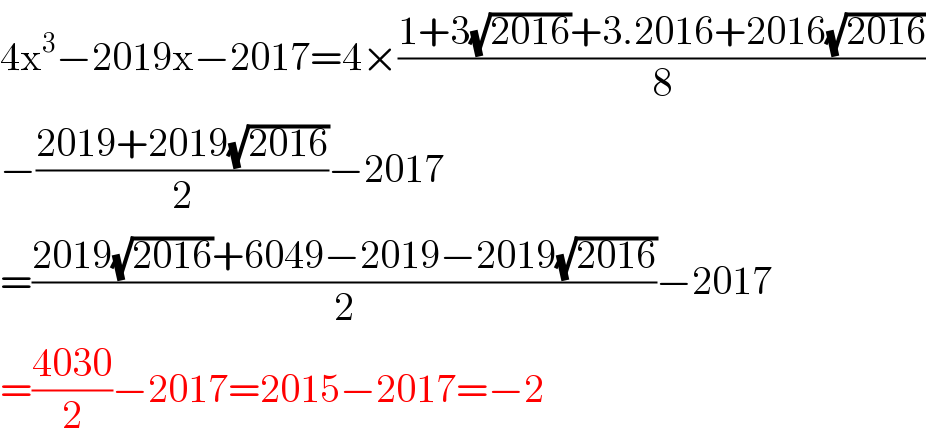
$$\mathrm{4x}^{\mathrm{3}} −\mathrm{2019x}−\mathrm{2017}=\mathrm{4}×\frac{\mathrm{1}+\mathrm{3}\sqrt{\mathrm{2016}}+\mathrm{3}.\mathrm{2016}+\mathrm{2016}\sqrt{\mathrm{2016}}}{\mathrm{8}} \\ $$$$−\frac{\mathrm{2019}+\mathrm{2019}\sqrt{\mathrm{2016}}}{\mathrm{2}}−\mathrm{2017} \\ $$$$=\frac{\mathrm{2019}\sqrt{\mathrm{2016}}+\mathrm{6049}−\mathrm{2019}−\mathrm{2019}\sqrt{\mathrm{2016}}}{\mathrm{2}}−\mathrm{2017} \\ $$$$=\frac{\mathrm{4030}}{\mathrm{2}}−\mathrm{2017}=\mathrm{2015}−\mathrm{2017}=−\mathrm{2} \\ $$
Commented by Aina Samuel Temidayo last updated on 04/Sep/20

$$\mathrm{Thanks}. \\ $$
