Question Number 45283 by peter frank last updated on 11/Oct/18
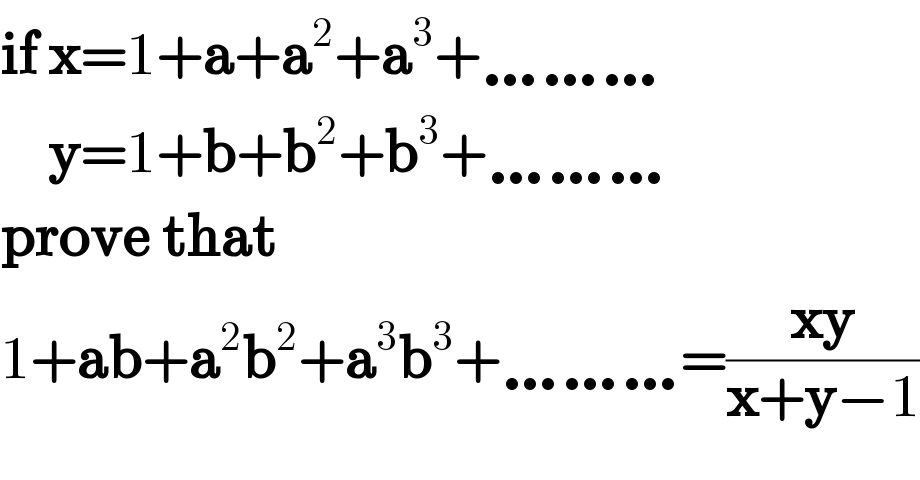
$$\boldsymbol{\mathrm{if}}\:\boldsymbol{\mathrm{x}}=\mathrm{1}+\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{a}}^{\mathrm{3}} +\ldots\ldots\ldots \\ $$$$\:\:\:\:\boldsymbol{\mathrm{y}}=\mathrm{1}+\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{b}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{3}} +\ldots\ldots\ldots \\ $$$$\boldsymbol{\mathrm{prove}}\:\boldsymbol{\mathrm{that}} \\ $$$$\mathrm{1}+\boldsymbol{\mathrm{ab}}+\boldsymbol{\mathrm{a}}^{\mathrm{2}} \boldsymbol{\mathrm{b}}^{\mathrm{2}} +\boldsymbol{\mathrm{a}}^{\mathrm{3}} \boldsymbol{\mathrm{b}}^{\mathrm{3}} +\ldots\ldots\ldots=\frac{\boldsymbol{\mathrm{xy}}}{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}−\mathrm{1}} \\ $$
Answered by ajfour last updated on 11/Oct/18
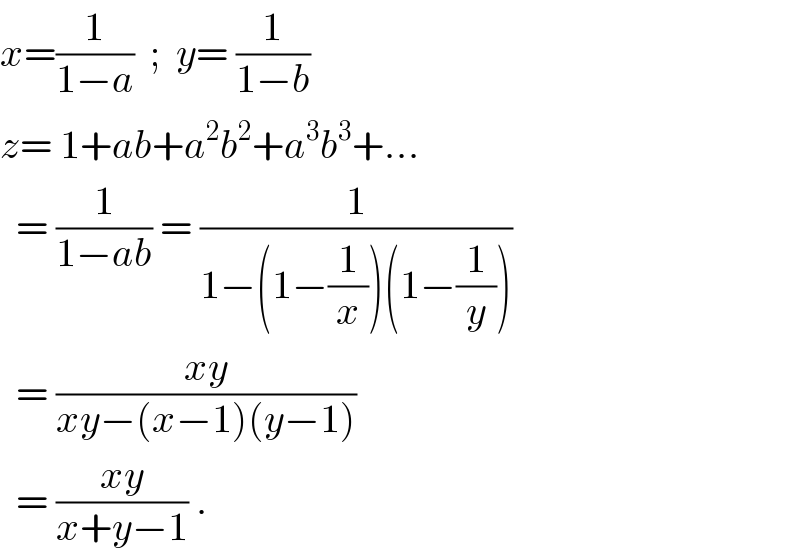
$${x}=\frac{\mathrm{1}}{\mathrm{1}−{a}}\:\:;\:\:{y}=\:\frac{\mathrm{1}}{\mathrm{1}−{b}} \\ $$$${z}=\:\mathrm{1}+{ab}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{a}^{\mathrm{3}} {b}^{\mathrm{3}} +… \\ $$$$\:\:=\:\frac{\mathrm{1}}{\mathrm{1}−{ab}}\:=\:\frac{\mathrm{1}}{\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{{y}}\right)} \\ $$$$\:\:=\:\frac{{xy}}{{xy}−\left({x}−\mathrm{1}\right)\left({y}−\mathrm{1}\right)} \\ $$$$\:\:=\:\frac{{xy}}{{x}+{y}−\mathrm{1}}\:. \\ $$
Commented by peter frank last updated on 11/Oct/18
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by maxmathsup by imad last updated on 11/Oct/18
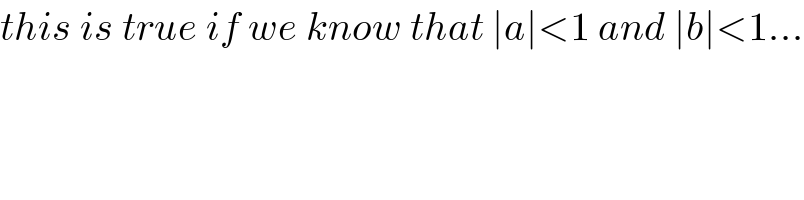
$${this}\:{is}\:{true}\:{if}\:{we}\:{know}\:{that}\:\mid{a}\mid<\mathrm{1}\:{and}\:\mid{b}\mid<\mathrm{1}… \\ $$
