If-x-1-x-2-x-0-prove-that-x-n-1-x-n-2-n-Z-

Question Number 108516 by Rasheed.Sindhi last updated on 17/Aug/20

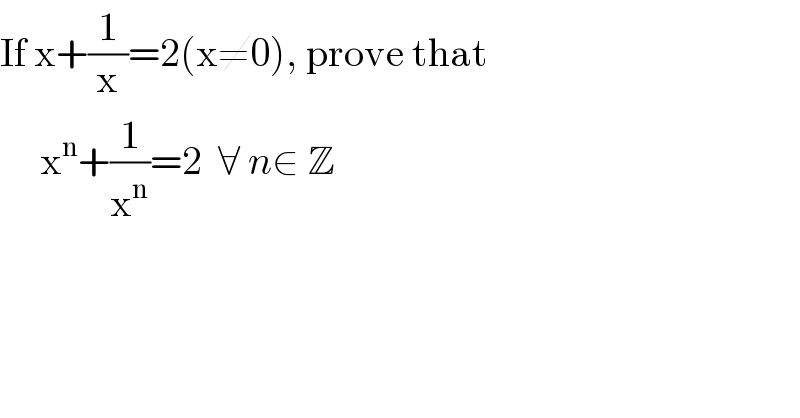
$$\mathrm{If}\:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{2}\left(\mathrm{x}\neq\mathrm{0}\right),\:\mathrm{prove}\:\mathrm{that} \\ $$$$\:\:\:\:\:\mathrm{x}^{\mathrm{n}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{n}} }=\mathrm{2}\:\:\forall\:{n}\in\:\mathbb{Z} \\ $$

Commented by mr W last updated on 17/Aug/20

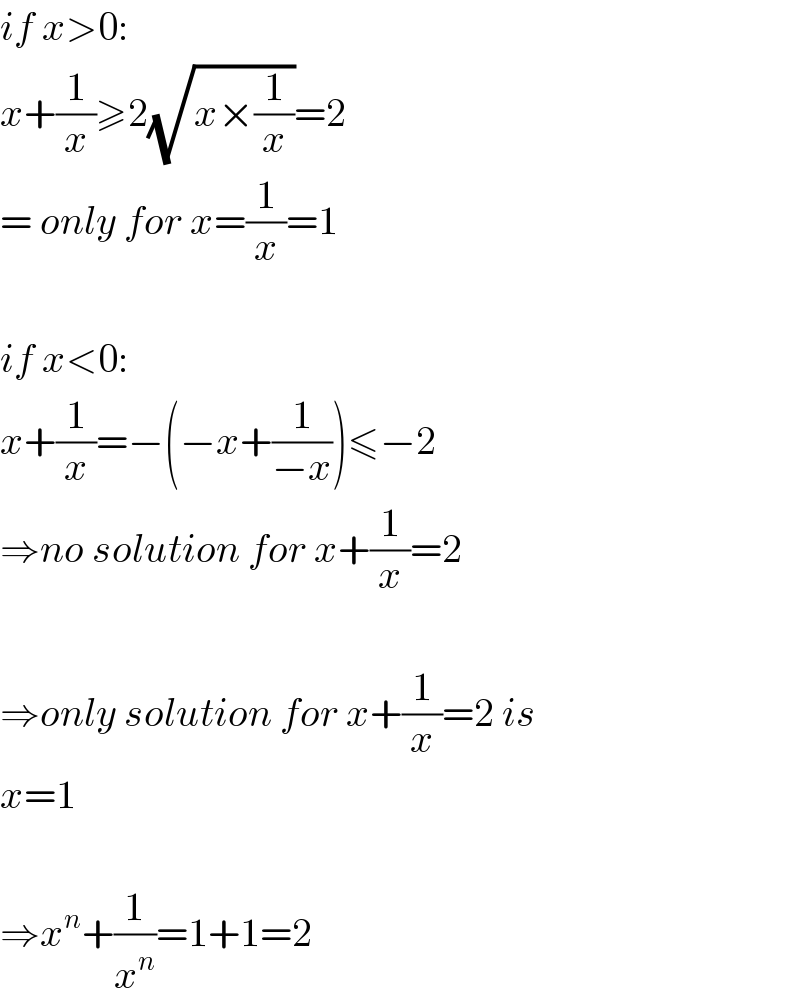
if x>0: x+(1/x)≥2(√(x×(1/x)))=2 = only for x=(1/x)=1 if x<0: x+(1/x)=−(−x+(1/(−x)))≤−2 ⇒no solution for x+(1/x)=2 ⇒only solution for x+(1/x)=2 is x=1 ⇒x^n +(1/x^n )=1+1=2

$${if}\:{x}>\mathrm{0}: \\ $$$${x}+\frac{\mathrm{1}}{{x}}\geqslant\mathrm{2}\sqrt{{x}×\frac{\mathrm{1}}{{x}}}=\mathrm{2} \\ $$$$=\:{only}\:{for}\:{x}=\frac{\mathrm{1}}{{x}}=\mathrm{1} \\ $$$$ \\ $$$${if}\:{x}<\mathrm{0}: \\ $$$${x}+\frac{\mathrm{1}}{{x}}=−\left(−{x}+\frac{\mathrm{1}}{−{x}}\right)\leqslant−\mathrm{2} \\ $$$$\Rightarrow{no}\:{solution}\:{for}\:{x}+\frac{\mathrm{1}}{{x}}=\mathrm{2} \\ $$$$ \\ $$$$\Rightarrow{only}\:{solution}\:{for}\:{x}+\frac{\mathrm{1}}{{x}}=\mathrm{2}\:{is} \\ $$$${x}=\mathrm{1} \\ $$$$ \\ $$$$\Rightarrow{x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }=\mathrm{1}+\mathrm{1}=\mathrm{2} \\ $$

Commented by Rasheed.Sindhi last updated on 17/Aug/20

$$\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} \mathrm{cellent}! \\ $$

Commented by udaythool last updated on 17/Aug/20

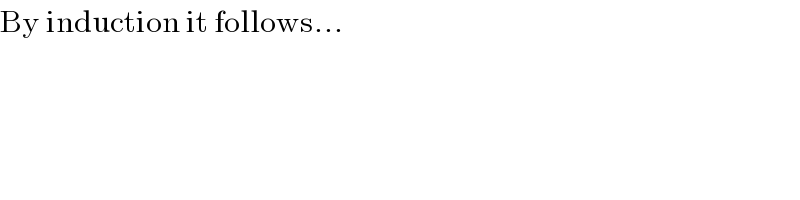
$$\mathrm{By}\:\mathrm{induction}\:\mathrm{it}\:\mathrm{follows}… \\ $$

Commented by Rasheed.Sindhi last updated on 17/Aug/20

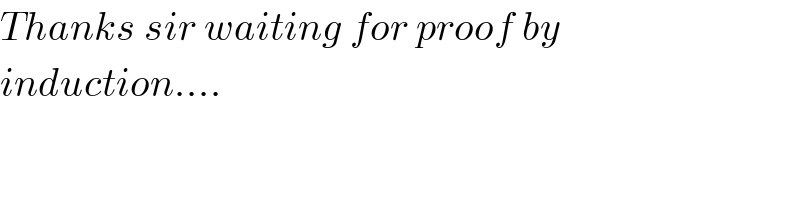
$${Thanks}\:{sir}\:{waiting}\:{for}\:{proof}\:{by} \\ $$$${induction}…. \\ $$

Commented by udaythool last updated on 17/Aug/20

Let n=0,1,... Induction statment: P_n : x^n +(1/x^n )=2 For n=0 and 1, P_n is true Induction hypothesis: Let P_n is true for all n=0,..., k ∴(x^(k+1) +(1/x^(k+1) ))=(x+(1/x))(x^k +(1/x^k ))−2=2x2−2=2 i.e. P_k ⇒P_(k+1) Thus by PI P_n is true for all n∈Z^+ If n∈Z^− ⇒n=−m for m=∣n∣∈Z^+ ∴ x^n +(1/x^n )=x^(−m) +(1/x^(−m) )=x^m +(1/x^m )=2 And hence P_n is true ∀n∈Z etc...

$$\mathrm{Let}\:{n}=\mathrm{0},\mathrm{1},… \\ $$$$\mathrm{Induction}\:\mathrm{statment}: \\ $$$${P}_{\mathrm{n}} :\:{x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }=\mathrm{2} \\ $$$$\mathrm{For}\:{n}=\mathrm{0}\:\mathrm{and}\:\mathrm{1},\:{P}_{{n}} \:\mathrm{is}\:\mathrm{true} \\ $$$$\mathrm{Induction}\:\mathrm{hypothesis}: \\ $$$$\mathrm{Let}\:{P}_{{n}} \:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:\mathrm{all}\:{n}=\mathrm{0},…,\:{k} \\ $$$$\therefore\left({x}^{{k}+\mathrm{1}} +\frac{\mathrm{1}}{{x}^{{k}+\mathrm{1}} }\right)=\left({x}+\frac{\mathrm{1}}{{x}}\right)\left({x}^{{k}} +\frac{\mathrm{1}}{{x}^{{k}} }\right)−\mathrm{2}=\mathrm{2×2}−\mathrm{2}=\mathrm{2} \\ $$$$\mathrm{i}.\mathrm{e}.\:{P}_{\mathrm{k}} \Rightarrow{P}_{{k}+\mathrm{1}} \\ $$$$\mathrm{Thus}\:\mathrm{by}\:\mathrm{PI}\:{P}_{{n}} \:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:\mathrm{all}\:{n}\in\mathbb{Z}^{+} \\ $$$$\mathrm{If}\:{n}\in\mathbb{Z}^{−} \Rightarrow{n}=−{m}\:\mathrm{for}\:{m}=\mid{n}\mid\in\mathbb{Z}^{+} \\ $$$$\therefore\:{x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }={x}^{−{m}} +\frac{\mathrm{1}}{{x}^{−{m}} }={x}^{{m}} +\frac{\mathrm{1}}{{x}^{{m}} }=\mathrm{2} \\ $$$$\mathrm{And}\:\mathrm{hence}\:{P}_{{n}} \:\mathrm{is}\:\mathrm{true}\:\forall{n}\in\mathbb{Z} \\ $$$$\mathrm{etc}… \\ $$$$ \\ $$

Commented by Rasheed.Sindhi last updated on 18/Aug/20

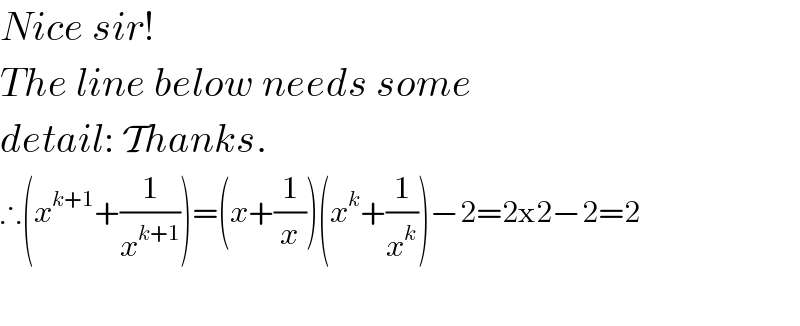
Nice sir! The line below needs some detail: Thanks. ∴(x^(k+1) +(1/x^(k+1) ))=(x+(1/x))(x^k +(1/x^k ))−2=2x2−2=2

$${Nice}\:{sir}!\: \\ $$$${The}\:{line}\:{below}\:{needs}\:{some} \\ $$$${detail}:\:\mathcal{T}{hanks}. \\ $$$$\therefore\left({x}^{{k}+\mathrm{1}} +\frac{\mathrm{1}}{{x}^{{k}+\mathrm{1}} }\right)=\left({x}+\frac{\mathrm{1}}{{x}}\right)\left({x}^{{k}} +\frac{\mathrm{1}}{{x}^{{k}} }\right)−\mathrm{2}=\mathrm{2×2}−\mathrm{2}=\mathrm{2} \\ $$$$ \\ $$

Commented by udaythool last updated on 13/Sep/20

Actually; (x+(1/x))(x^k +(1/x^k ))=(x^(k+1) +(1/x^(k+1) ))+(x^(k−1) +(1/x^(k−1) )) ⇒(x^(k+1) +(1/x^(k+1) ))=(x+(1/x))(x^k +(1/x^k ))−(x^(k−1) +(1/x^(k−1) )) we have assumed (induction hypothesis) p_n is true for n=k i.e. p_n =2 for n=1,2,…,k Thus (x^(k+1) +(1/x^(k+1) ))=2x2−2=2

$$\mathrm{Actually}; \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}}\right)\left({x}^{{k}} +\frac{\mathrm{1}}{{x}^{{k}} }\right)=\left({x}^{{k}+\mathrm{1}} +\frac{\mathrm{1}}{{x}^{{k}+\mathrm{1}} }\right)+\left({x}^{{k}−\mathrm{1}} +\frac{\mathrm{1}}{{x}^{{k}−\mathrm{1}} }\right) \\ $$$$\Rightarrow\left({x}^{{k}+\mathrm{1}} +\frac{\mathrm{1}}{{x}^{{k}+\mathrm{1}} }\right)=\left({x}+\frac{\mathrm{1}}{{x}}\right)\left({x}^{{k}} +\frac{\mathrm{1}}{{x}^{{k}} }\right)−\left({x}^{{k}−\mathrm{1}} +\frac{\mathrm{1}}{{x}^{{k}−\mathrm{1}} }\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{assumed}\:\left(\mathrm{induction}\right. \\ $$$$\left.\mathrm{hypothesis}\right)\:\mathrm{p}_{\mathrm{n}} \:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:\mathrm{n}=\mathrm{k} \\ $$$$\mathrm{i}.\mathrm{e}.\:\mathrm{p}_{\mathrm{n}} =\mathrm{2}\:\mathrm{for}\:\mathrm{n}=\mathrm{1},\mathrm{2},\ldots,\mathrm{k} \\ $$$$\mathrm{Thus}\:\left({x}^{{k}+\mathrm{1}} +\frac{\mathrm{1}}{{x}^{{k}+\mathrm{1}} }\right)=\mathrm{2×2}−\mathrm{2}=\mathrm{2} \\ $$

Answered by floor(10²Eta[1]) last updated on 17/Aug/20

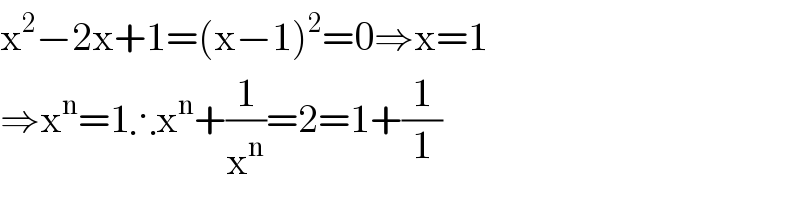
x^2 −2x+1=(x−1)^2 =0⇒x=1 ⇒x^n =1∴x^n +(1/x^n )=2=1+(1/1)

$$\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}=\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0}\Rightarrow\mathrm{x}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{n}} =\mathrm{1}\therefore\mathrm{x}^{\mathrm{n}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{n}} }=\mathrm{2}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}} \\ $$

Commented by Rasheed.Sindhi last updated on 17/Aug/20

$$\theta\alpha{n}\mathcal{X}\:{sir}! \\ $$

Answered by mathmax by abdo last updated on 17/Aug/20

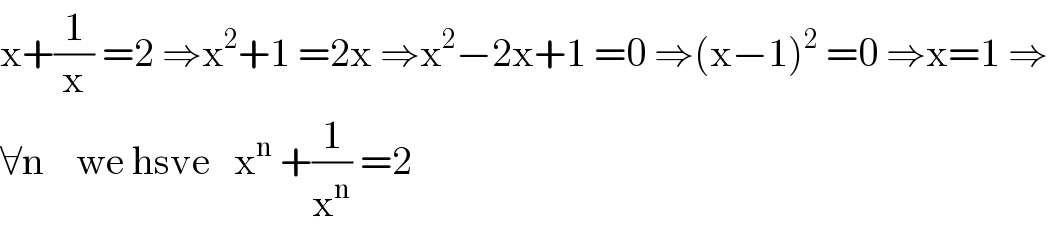
x+(1/x) =2 ⇒x^2 +1 =2x ⇒x^2 −2x+1 =0 ⇒(x−1)^2 =0 ⇒x=1 ⇒ ∀n we hsve x^n +(1/x^n ) =2

$$\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\:=\mathrm{2}\:\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{1}\:=\mathrm{2x}\:\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}\:=\mathrm{0}\:\Rightarrow\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \:=\mathrm{0}\:\Rightarrow\mathrm{x}=\mathrm{1}\:\Rightarrow \\ $$$$\forall\mathrm{n}\:\:\:\:\mathrm{we}\:\mathrm{hsve}\:\:\:\mathrm{x}^{\mathrm{n}} \:+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{n}} }\:=\mathrm{2} \\ $$

Commented by Rasheed.Sindhi last updated on 18/Aug/20

$${Thanx}\:{sir} \\ $$

Facebook Tweet Pin

If-x-1-x-2-x-0-prove-that-x-n-1-x-n-2-n-Z-

Leave a Reply Cancel reply