Question Number 51897 by Tawa1 last updated on 31/Dec/18

$$\mathrm{If}\:\:\:\:\mathrm{x}\:+\:\frac{\mathrm{1}}{\mathrm{x}}\:\:=\:\:\mathrm{2cos}\theta\:,\:\:\:\:\:\:\mathrm{y}\:+\:\frac{\mathrm{1}}{\mathrm{y}}\:\:=\:\:\mathrm{2cos}\phi\:,\:\:\:\:\:\:\:\:\:\mathrm{z}\:+\:\frac{\mathrm{1}}{\mathrm{z}}\:\:=\:\:\mathrm{2cos}\psi \\ $$$$\mathrm{Show}\:\mathrm{that}\:\:\:\:\:\:\:\:\:\:\mathrm{xyz}\:+\:\frac{\mathrm{1}}{\mathrm{xyz}}\:\:=\:\:\mathrm{2cos}\left(\theta\:+\:\phi\:+\:\psi\right) \\ $$
Answered by behi83417@gmail.com last updated on 31/Dec/18
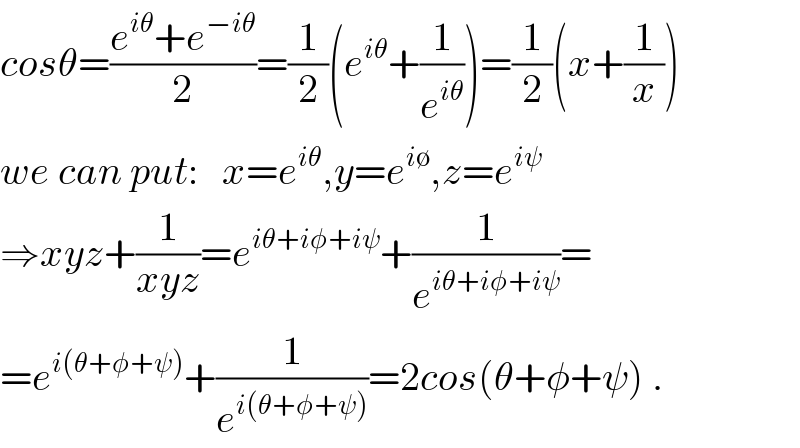
$${cos}\theta=\frac{{e}^{{i}\theta} +{e}^{−{i}\theta} }{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\left({e}^{{i}\theta} +\frac{\mathrm{1}}{{e}^{{i}\theta} }\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({x}+\frac{\mathrm{1}}{{x}}\right) \\ $$$${we}\:{can}\:{put}:\:\:\:{x}={e}^{{i}\theta} ,{y}={e}^{{i}\emptyset} ,{z}={e}^{{i}\psi} \\ $$$$\Rightarrow{xyz}+\frac{\mathrm{1}}{{xyz}}={e}^{{i}\theta+{i}\phi+{i}\psi} +\frac{\mathrm{1}}{{e}^{{i}\theta+{i}\phi+{i}\psi} }= \\ $$$$={e}^{{i}\left(\theta+\phi+\psi\right)} +\frac{\mathrm{1}}{{e}^{{i}\left(\theta+\phi+\psi\right)} }=\mathrm{2}{cos}\left(\theta+\phi+\psi\right)\:. \\ $$
Commented by Tawa1 last updated on 01/Jan/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
