Question Number 148890 by mathdanisur last updated on 01/Aug/21
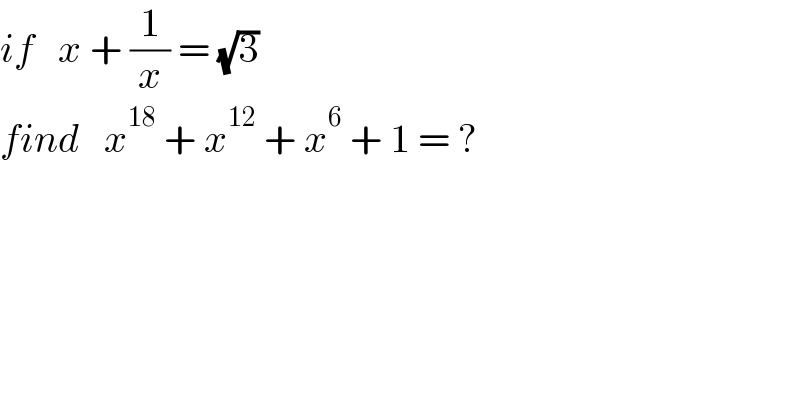
$${if}\:\:\:{x}\:+\:\frac{\mathrm{1}}{{x}}\:=\:\sqrt{\mathrm{3}} \\ $$$${find}\:\:\:{x}^{\mathrm{18}} \:+\:{x}^{\mathrm{12}} \:+\:{x}^{\mathrm{6}} \:+\:\mathrm{1}\:=\:? \\ $$
Answered by nimnim last updated on 01/Aug/21

$$\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}=\sqrt{\mathrm{3}}\Rightarrow\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{6}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{6}} }+\mathrm{3x}^{\mathrm{2}} .\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\left(\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)=\mathrm{1}\Rightarrow\mathrm{x}^{\mathrm{6}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{6}} }=−\mathrm{2} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{12}} +\mathrm{2x}^{\mathrm{6}} +\mathrm{1}=\mathrm{0}\:\:\:\:\Rightarrow\left(\mathrm{x}^{\mathrm{6}} +\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0}\:\:\Rightarrow\:\mathrm{x}^{\mathrm{6}} =−\mathrm{1} \\ $$$$\mathrm{Now},\:\mathrm{x}^{\mathrm{18}} +\mathrm{x}^{\mathrm{12}} +\mathrm{x}^{\mathrm{6}} +\mathrm{1}=\left(−\mathrm{1}\right)^{\mathrm{3}} +\left(−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\mathrm{1}+\mathrm{1}−\mathrm{1}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{0}\:\bigstar \\ $$
Commented by mathdanisur last updated on 01/Aug/21

$${Thank}\:{you}\:{Ser} \\ $$
