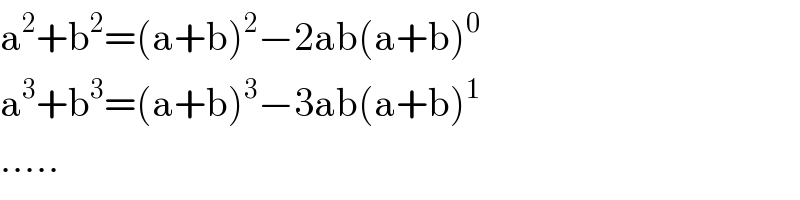if-x-1-x-a-a-R-find-x-n-1-x-n-n-N-

Question Number 80243 by mr W last updated on 01/Feb/20

i f x + \frac{1}{x} = a (a \in R)

f i n d x^{n} + \frac{1}{x^{n}} = ?

(n \in N)

Commented by TawaTawa last updated on 01/Feb/20

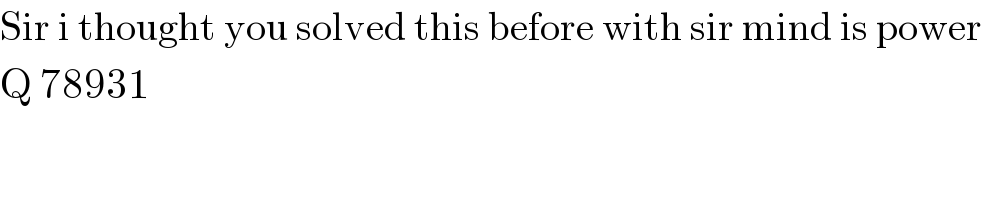
Sir i thought you solved this before with sir mind is power

Q 78931

Commented by TawaTawa last updated on 01/Feb/20

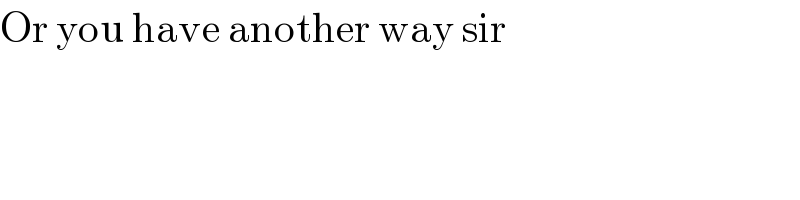
Or you have another way sir

Commented by TawaTawa last updated on 01/Feb/20

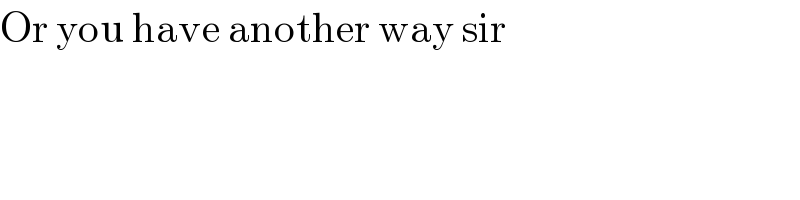
Or you have another way sir

Commented by behi83417@gmail.com last updated on 01/Feb/20

sir mrW! what do think about this ?

a^{n} + b^{n} = {(a + b)}^{n} - nab {(a + b)}^{n - 2} [n ⩾ 2]

Commented by behi83417@gmail.com last updated on 01/Feb/20

i mean that : is this true ? or can we prove

it ?

Commented by mr W last updated on 01/Feb/20

n o s i r,

a^{n} + b^{n} = {(a + b)}^{n} - nab {(a + b)}^{n - 2} [n ⩾ 2]

i s n o t t r u e .

Commented by behi83417@gmail.com last updated on 01/Feb/20

a^{2} + b^{2} = {(a + b)}^{2} - 2 ab {(a + b)}^{0}

a^{3} + b^{3} = {(a + b)}^{3} - 3 ab {(a + b)}^{1}

\dots . .