Question Number 20831 by j.masanja06@gmail.com last updated on 04/Sep/17
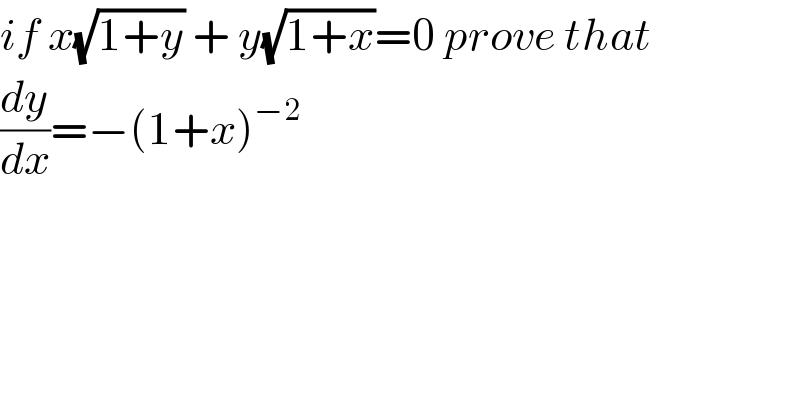
$${if}\:{x}\sqrt{\mathrm{1}+{y}}\:+\:{y}\sqrt{\mathrm{1}+{x}}=\mathrm{0}\:{prove}\:{that}\: \\ $$$$\frac{{dy}}{{dx}}=−\left(\mathrm{1}+{x}\right)^{−\mathrm{2}} \\ $$
Answered by ajfour last updated on 04/Sep/17
![x(√(1+y)) =−y(√(1+x)) so x^2 (1+y)=y^2 (1+x) or x^2 −y^2 =xy(y−x) ⇒ if y≠x , x+y+xy=0 or y=−(x/(1+x)) differentiating which we get (dy/dx)=−(([(1+x)−x])/((1+x)^2 )) = −(1+x)^(−2) .](https://www.tinkutara.com/question/Q20834.png)
$${x}\sqrt{\mathrm{1}+{y}}\:=−{y}\sqrt{\mathrm{1}+{x}}\: \\ $$$${so} \\ $$$${x}^{\mathrm{2}} \left(\mathrm{1}+{y}\right)={y}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)\:\:\: \\ $$$${or}\:\:\:{x}^{\mathrm{2}} −{y}^{\mathrm{2}} ={xy}\left({y}−{x}\right) \\ $$$$\Rightarrow\:\:\:\:{if}\:{y}\neq{x}\:,\:\:\:{x}+{y}+{xy}=\mathrm{0}\:\: \\ $$$${or}\:\:\:\:{y}=−\frac{{x}}{\mathrm{1}+{x}} \\ $$$${differentiating}\:{which}\:{we}\:{get} \\ $$$$\:\:\:\frac{{dy}}{{dx}}=−\frac{\left[\left(\mathrm{1}+{x}\right)−{x}\right]}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }\:=\:−\left(\mathrm{1}+{x}\right)^{−\mathrm{2}} \:. \\ $$
