Question Number 152772 by Rankut last updated on 01/Sep/21
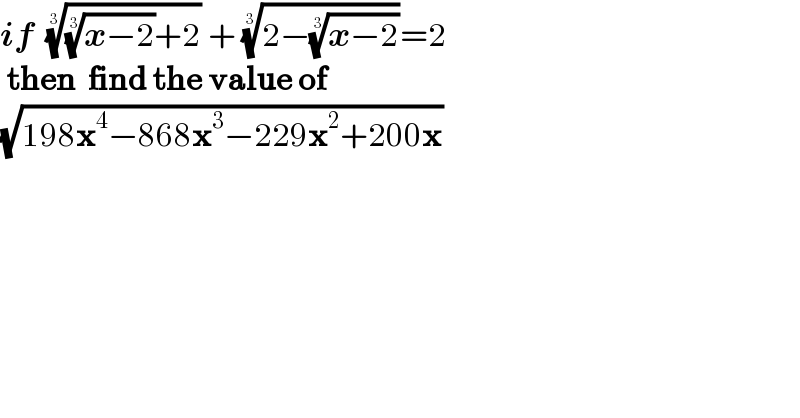
$$\boldsymbol{{if}}\:\:\sqrt[{\mathrm{3}}]{\sqrt[{\mathrm{3}}]{\boldsymbol{{x}}−\mathrm{2}}+\mathrm{2}}\:+\:\sqrt[{\mathrm{3}}]{\mathrm{2}−\sqrt[{\mathrm{3}}]{\boldsymbol{{x}}−\mathrm{2}}}=\mathrm{2} \\ $$$$\:\boldsymbol{\mathrm{then}}\:\:\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{value}}\:\boldsymbol{\mathrm{of}}\: \\ $$$$\sqrt{\mathrm{198}\boldsymbol{\mathrm{x}}^{\mathrm{4}} −\mathrm{868}\boldsymbol{\mathrm{x}}^{\mathrm{3}} −\mathrm{229}\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{200}\boldsymbol{\mathrm{x}}} \\ $$
Commented by Rankut last updated on 01/Sep/21

$${any}\:{help}\:{please} \\ $$
Commented by MJS_new last updated on 01/Sep/21

$$\mathrm{typo}? \\ $$$$\mathrm{there}'\mathrm{s}\:\mathrm{a}\:\mathrm{similae}\:\mathrm{question}…\:\mathrm{just}\:\mathrm{scroll}\:\mathrm{down} \\ $$$$\mathrm{to}\:\mathrm{find}\:\mathrm{it} \\ $$
Answered by mr W last updated on 01/Sep/21
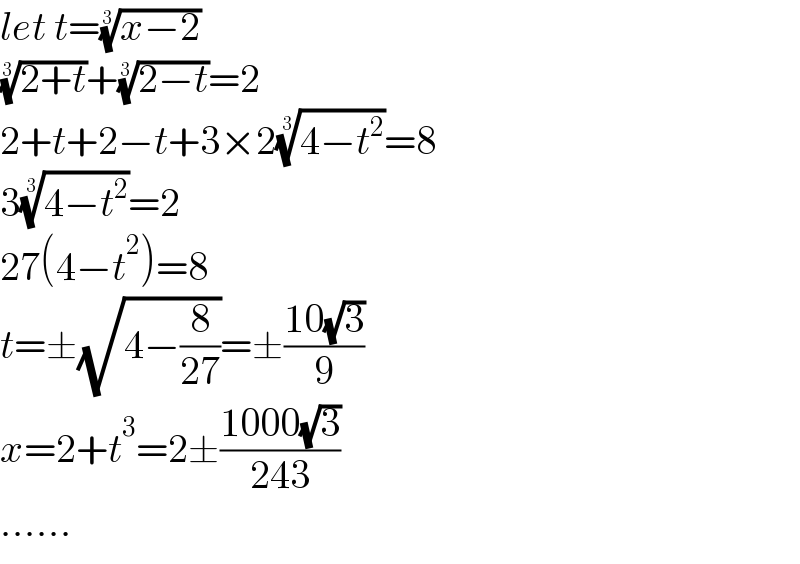
$${let}\:{t}=\sqrt[{\mathrm{3}}]{{x}−\mathrm{2}} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{2}+{t}}+\sqrt[{\mathrm{3}}]{\mathrm{2}−{t}}=\mathrm{2} \\ $$$$\mathrm{2}+{t}+\mathrm{2}−{t}+\mathrm{3}×\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{4}−{t}^{\mathrm{2}} }=\mathrm{8} \\ $$$$\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{4}−{t}^{\mathrm{2}} }=\mathrm{2} \\ $$$$\mathrm{27}\left(\mathrm{4}−{t}^{\mathrm{2}} \right)=\mathrm{8} \\ $$$${t}=\pm\sqrt{\mathrm{4}−\frac{\mathrm{8}}{\mathrm{27}}}=\pm\frac{\mathrm{10}\sqrt{\mathrm{3}}}{\mathrm{9}} \\ $$$${x}=\mathrm{2}+{t}^{\mathrm{3}} =\mathrm{2}\pm\frac{\mathrm{1000}\sqrt{\mathrm{3}}}{\mathrm{243}} \\ $$$$…… \\ $$
Commented by Rankut last updated on 01/Sep/21

$${thank}\:{you}\:{sir} \\ $$
