Question Number 92426 by Jidda28 last updated on 06/May/20
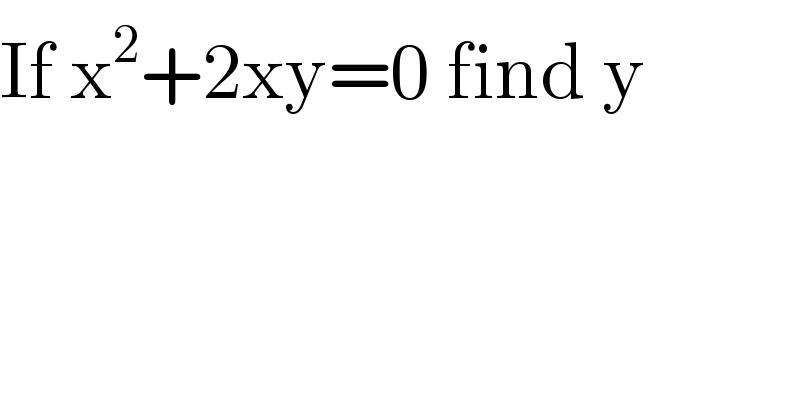
$$\mathrm{If}\:\mathrm{x}^{\mathrm{2}} +\mathrm{2xy}=\mathrm{0}\:\mathrm{find}\:\mathrm{y} \\ $$
Commented by Jidda28 last updated on 07/May/20
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{sir} \\ $$
Commented by Rio Michael last updated on 06/May/20

$$\mathrm{sir}\:\mathrm{please}\:\mathrm{reduce}\:\mathrm{your}\:\mathrm{font}\:\mathrm{sizes}\:\mathrm{alittle} \\ $$$$\boldsymbol{\mathrm{solution}} \\ $$$$\:{x}^{\mathrm{2}} \:+\mathrm{2}{xy}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:{x}\left({x}+\mathrm{2}{y}\right)\:=\:\mathrm{0} \\ $$$$\mathrm{either}\:{x}\:=\:\mathrm{0}\:\mathrm{or}\:{x}\:+\:\mathrm{2}{y}\:=\:\mathrm{0} \\ $$$$\:\:\:{y}\:=\:−\frac{{x}}{\mathrm{2}} \\ $$$$\Rightarrow\:{y}\:=\:\mathrm{0} \\ $$
Commented by Jidda28 last updated on 06/May/20
$$\mathrm{ok}\:\mathrm{sir}\:\mathrm{thank}\:\mathrm{for}\:\mathrm{the}\:\mathrm{solution} \\ $$
Commented by MJS last updated on 07/May/20
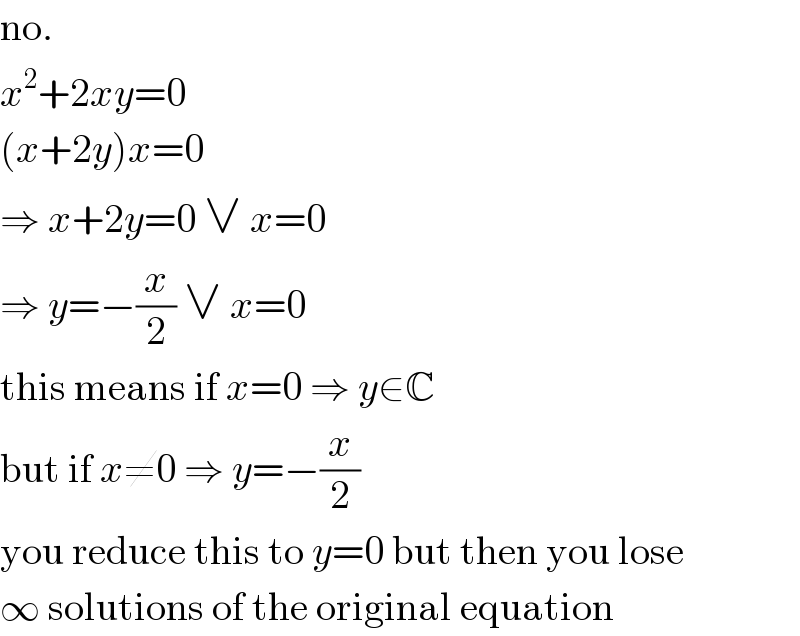
$$\mathrm{no}. \\ $$$${x}^{\mathrm{2}} +\mathrm{2}{xy}=\mathrm{0} \\ $$$$\left({x}+\mathrm{2}{y}\right){x}=\mathrm{0} \\ $$$$\Rightarrow\:{x}+\mathrm{2}{y}=\mathrm{0}\:\vee\:{x}=\mathrm{0} \\ $$$$\Rightarrow\:{y}=−\frac{{x}}{\mathrm{2}}\:\vee\:{x}=\mathrm{0} \\ $$$$\mathrm{this}\:\mathrm{means}\:\mathrm{if}\:{x}=\mathrm{0}\:\Rightarrow\:{y}\in\mathbb{C} \\ $$$$\mathrm{but}\:\mathrm{if}\:{x}\neq\mathrm{0}\:\Rightarrow\:{y}=−\frac{{x}}{\mathrm{2}} \\ $$$$\mathrm{you}\:\mathrm{reduce}\:\mathrm{this}\:\mathrm{to}\:{y}=\mathrm{0}\:\mathrm{but}\:\mathrm{then}\:\mathrm{you}\:\mathrm{lose} \\ $$$$\infty\:\mathrm{solutions}\:\mathrm{of}\:\mathrm{the}\:\mathrm{original}\:\mathrm{equation} \\ $$
