Question Number 151315 by mathdanisur last updated on 20/Aug/21
![if x^2 +y^2 =16^2 ; y^2 +z^2 =24^2 z^2 +t^2 =42^2 and t^2 +x^2 =38^2 find max[(x+z)(y+t)]=?](https://www.tinkutara.com/question/Q151315.png)
$$\mathrm{if}\:\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{16}^{\mathrm{2}} \:\:;\:\:\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} =\mathrm{24}^{\mathrm{2}} \\ $$$$\mathrm{z}^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} =\mathrm{42}^{\mathrm{2}} \:\:\mathrm{and}\:\:\mathrm{t}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} =\mathrm{38}^{\mathrm{2}} \\ $$$$\mathrm{find}\:\:\mathrm{max}\left[\left(\mathrm{x}+\mathrm{z}\right)\left(\mathrm{y}+\mathrm{t}\right)\right]=? \\ $$
Answered by dumitrel last updated on 20/Aug/21
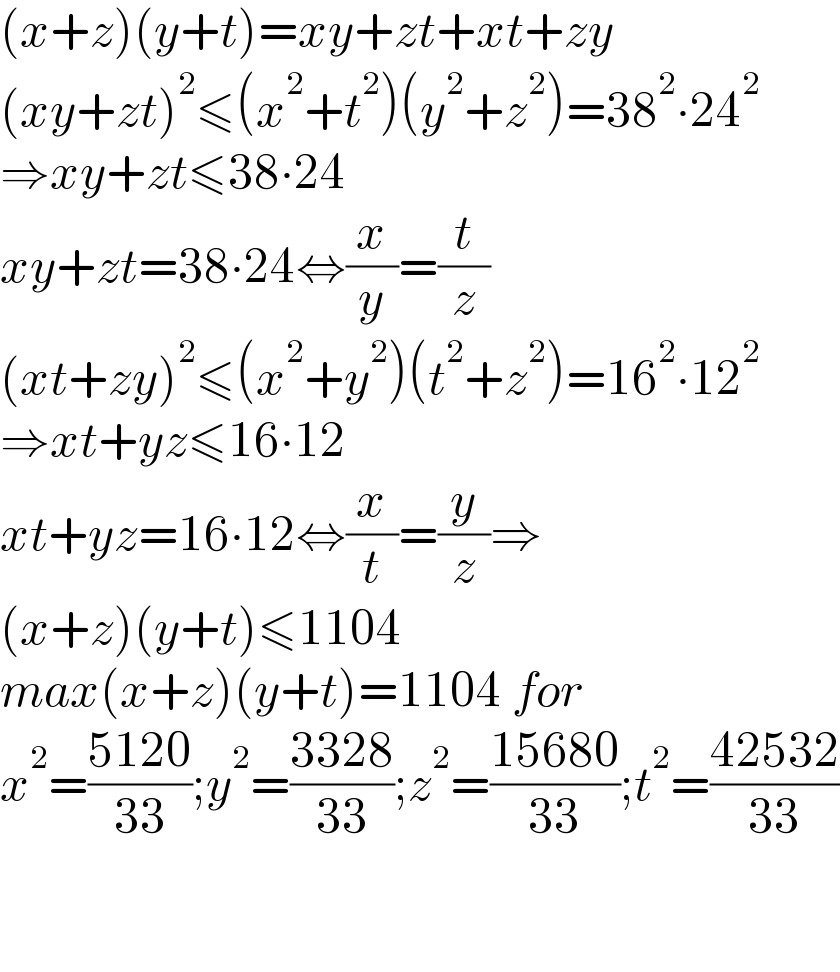
$$\left({x}+{z}\right)\left({y}+{t}\right)={xy}+{zt}+{xt}+{zy} \\ $$$$\left({xy}+{zt}\right)^{\mathrm{2}} \leqslant\left({x}^{\mathrm{2}} +{t}^{\mathrm{2}} \right)\left({y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)=\mathrm{38}^{\mathrm{2}} \centerdot\mathrm{24}^{\mathrm{2}} \\ $$$$\Rightarrow{xy}+{zt}\leqslant\mathrm{38}\centerdot\mathrm{24} \\ $$$${xy}+{zt}=\mathrm{38}\centerdot\mathrm{24}\Leftrightarrow\frac{{x}}{{y}}=\frac{{t}}{{z}} \\ $$$$\left({xt}+{zy}\right)^{\mathrm{2}} \leqslant\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\left({t}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)=\mathrm{16}^{\mathrm{2}} \centerdot\mathrm{12}^{\mathrm{2}} \\ $$$$\Rightarrow{xt}+{yz}\leqslant\mathrm{16}\centerdot\mathrm{12} \\ $$$${xt}+{yz}=\mathrm{16}\centerdot\mathrm{12}\Leftrightarrow\frac{{x}}{{t}}=\frac{{y}}{{z}}\Rightarrow \\ $$$$\left({x}+{z}\right)\left({y}+{t}\right)\leqslant\mathrm{1104} \\ $$$${max}\left({x}+{z}\right)\left({y}+{t}\right)=\mathrm{1104}\:{for} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{5120}}{\mathrm{33}};{y}^{\mathrm{2}} =\frac{\mathrm{3328}}{\mathrm{33}};{z}^{\mathrm{2}} =\frac{\mathrm{15680}}{\mathrm{33}};{t}^{\mathrm{2}} =\frac{\mathrm{42532}}{\mathrm{33}} \\ $$$$ \\ $$$$ \\ $$
Commented by mathdanisur last updated on 20/Aug/21
$$\mathrm{Thank}\:\mathrm{You}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{cool} \\ $$
