Menu Close

if-x-3-1-x-3-52-find-the-value-of-x-4-1-x-4-

Tinku Tara 0 Comments
Pin




Question Number 119193 by mr W last updated on 22/Oct/20
if x^3 +(1/x^3 )=52, find the value of x^4 +(1/x^4 )=?
$${if}\:{x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }=\mathrm{52},\:{find}\:{the}\:{value}\:{of} \\ $$$${x}^{\mathrm{4}} +\frac{\mathrm{1}}{{x}^{\mathrm{4}} }=? \\ $$
Commented by PRITHWISH SEN 2 last updated on 22/Oct/20
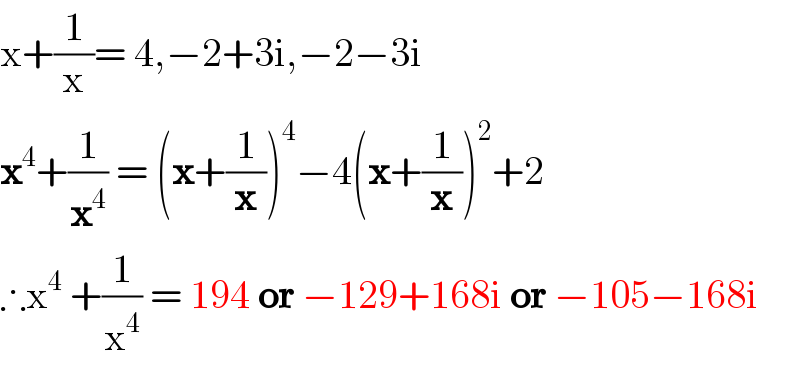
x+(1/x)= 4,−2+3i,−2−3i x^4 +(1/x^4 ) = (x+(1/x))^4 −4(x+(1/x))^2 +2 ∴x^4 +(1/x^4 ) = 194 or −129+168i or −105−168i
$$\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}=\:\mathrm{4},−\mathrm{2}+\mathrm{3i},−\mathrm{2}−\mathrm{3i} \\ $$$$\boldsymbol{\mathrm{x}}^{\mathrm{4}} +\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}^{\mathrm{4}} }\:=\:\left(\boldsymbol{\mathrm{x}}+\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}\right)^{\mathrm{4}} −\mathrm{4}\left(\boldsymbol{\mathrm{x}}+\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}\right)^{\mathrm{2}} +\mathrm{2} \\ $$$$\therefore\mathrm{x}^{\mathrm{4}} \:+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{4}} }\:=\:\mathrm{194}\:\boldsymbol{\mathrm{or}}\:−\mathrm{129}+\mathrm{168i}\:\boldsymbol{\mathrm{or}}\:−\mathrm{105}−\mathrm{168i} \\ $$
Commented by mr W last updated on 22/Oct/20
thanks!
$${thanks}! \\ $$
Commented by PRITHWISH SEN 2 last updated on 22/Oct/20
welcome
$$\mathrm{welcome}\: \\ $$
Answered by TANMAY PANACEA last updated on 22/Oct/20
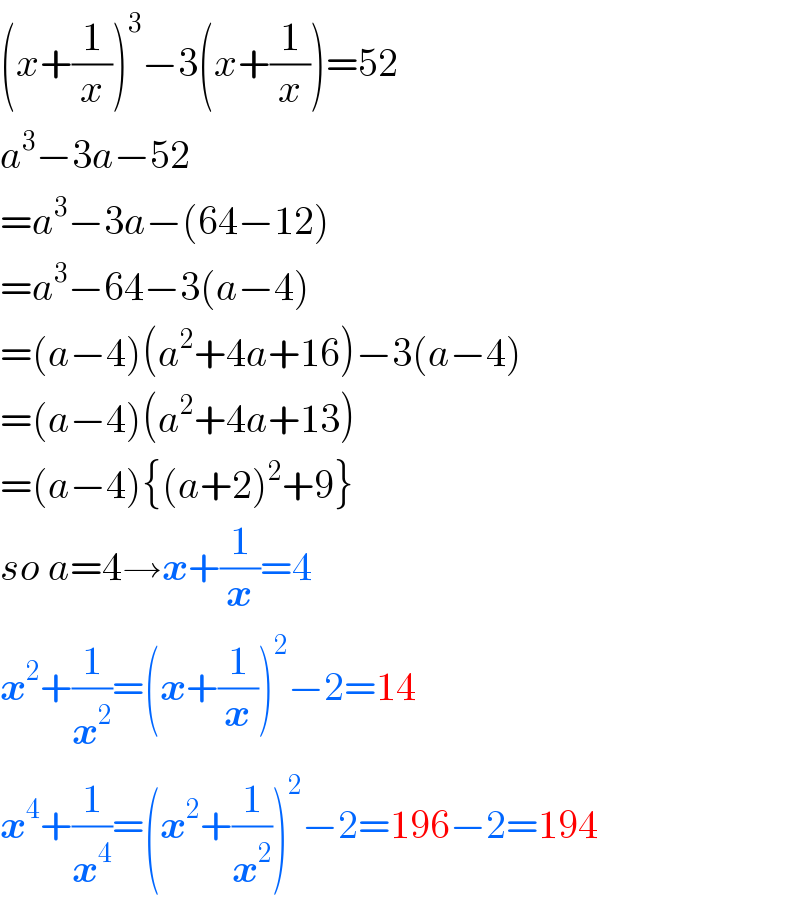
(x+(1/x))^3 −3(x+(1/x))=52 a^3 −3a−52 =a^3 −3a−(64−12) =a^3 −64−3(a−4) =(a−4)(a^2 +4a+16)−3(a−4) =(a−4)(a^2 +4a+13) =(a−4){(a+2)^2 +9} so a=4→x+(1/x)=4 x^2 +(1/x^2 )=(x+(1/x))^2 −2=14 x^4 +(1/x^4 )=(x^2 +(1/x^2 ))^2 −2=196−2=194
$$\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{3}} −\mathrm{3}\left({x}+\frac{\mathrm{1}}{{x}}\right)=\mathrm{52} \\ $$$${a}^{\mathrm{3}} −\mathrm{3}{a}−\mathrm{52} \\ $$$$={a}^{\mathrm{3}} −\mathrm{3}{a}−\left(\mathrm{64}−\mathrm{12}\right) \\ $$$$={a}^{\mathrm{3}} −\mathrm{64}−\mathrm{3}\left({a}−\mathrm{4}\right) \\ $$$$=\left({a}−\mathrm{4}\right)\left({a}^{\mathrm{2}} +\mathrm{4}{a}+\mathrm{16}\right)−\mathrm{3}\left({a}−\mathrm{4}\right) \\ $$$$=\left({a}−\mathrm{4}\right)\left({a}^{\mathrm{2}} +\mathrm{4}{a}+\mathrm{13}\right) \\ $$$$=\left({a}−\mathrm{4}\right)\left\{\left({a}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{9}\right\} \\ $$$${so}\:{a}=\mathrm{4}\rightarrow\boldsymbol{{x}}+\frac{\mathrm{1}}{\boldsymbol{{x}}}=\mathrm{4} \\ $$$$\boldsymbol{{x}}^{\mathrm{2}} +\frac{\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{2}} }=\left(\boldsymbol{{x}}+\frac{\mathrm{1}}{\boldsymbol{{x}}}\right)^{\mathrm{2}} −\mathrm{2}=\mathrm{14} \\ $$$$\boldsymbol{{x}}^{\mathrm{4}} +\frac{\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{4}} }=\left(\boldsymbol{{x}}^{\mathrm{2}} +\frac{\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{2}} }\right)^{\mathrm{2}} −\mathrm{2}=\mathrm{196}−\mathrm{2}=\mathrm{194} \\ $$
Commented by mr W last updated on 22/Oct/20
correct, thanks!
$${correct},\:{thanks}! \\ $$
Commented by TANMAY PANACEA last updated on 22/Oct/20
sir i have not considered comlex solution
$${sir}\:{i}\:{have}\:{not}\:{considered}\:{comlex}\:{solution} \\ $$
Answered by 1549442205PVT last updated on 23/Oct/20
x^3 +(1/x^3 )=52⇔x^6 −52x^3 +1=0 Δ′=26^2 −1=675=(15(√3))^2 ⇒x^3 =26±15(√3) =(2±(√3) )^3 ⇒x=2±(√3) Since (2+(√3))(2−(√3))=1⇒x+(1/x) =2+(√3)+2−(√3)=4 ⇒(x^4 +(1/x^4 ))=(x^2 +(1/x^2 ))−2=[(x+(1/x))^2 −2]^2 −2 =(4^2 −2)^2 −2=14^2 −2=194
$${x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }=\mathrm{52}\Leftrightarrow\mathrm{x}^{\mathrm{6}} −\mathrm{52x}^{\mathrm{3}} +\mathrm{1}=\mathrm{0} \\ $$$$\Delta'=\mathrm{26}^{\mathrm{2}} −\mathrm{1}=\mathrm{675}=\left(\mathrm{15}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{3}} =\mathrm{26}\pm\mathrm{15}\sqrt{\mathrm{3}}\:=\left(\mathrm{2}\pm\sqrt{\mathrm{3}}\:\right)^{\mathrm{3}} \Rightarrow\mathrm{x}=\mathrm{2}\pm\sqrt{\mathrm{3}} \\ $$$$\mathrm{Since}\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)=\mathrm{1}\Rightarrow\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}} \\ $$$$=\mathrm{2}+\sqrt{\mathrm{3}}+\mathrm{2}−\sqrt{\mathrm{3}}=\mathrm{4} \\ $$$$\Rightarrow\left(\mathrm{x}^{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{4}} }\right)=\left(\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)−\mathrm{2}=\left[\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} −\mathrm{2}\right]^{\mathrm{2}} −\mathrm{2} \\ $$$$=\left(\mathrm{4}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}=\mathrm{14}^{\mathrm{2}} −\mathrm{2}=\mathrm{194} \\ $$
Answered by malwan last updated on 24/Oct/20
x^6 −52x^3 +1=0 this equation has 6 solutions 4 complex and 2 real x=2±(√3) x=2+(√3) ⇒x^4 +(1/x^4 ) = (97+56(√3))+((1/(97+56(√3)))) =(97+56(√3))+(((97−56(√3))/(9409−9408))) =97+97= 194 and the same way x=2−(√3) ⇒x^4 +(1/x^4 ) = 194
$${x}^{\mathrm{6}} −\mathrm{52}{x}^{\mathrm{3}} +\mathrm{1}=\mathrm{0} \\ $$$${this}\:{equation}\:{has}\:\mathrm{6}\:{solutions} \\ $$$$\mathrm{4}\:{complex} \\ $$$${and}\:\mathrm{2}\:{real}\:{x}=\mathrm{2}\pm\sqrt{\mathrm{3}} \\ $$$${x}=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$$\Rightarrow{x}^{\mathrm{4}} +\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\:=\:\left(\mathrm{97}+\mathrm{56}\sqrt{\mathrm{3}}\right)+\left(\frac{\mathrm{1}}{\mathrm{97}+\mathrm{56}\sqrt{\mathrm{3}}}\right) \\ $$$$=\left(\mathrm{97}+\mathrm{56}\sqrt{\mathrm{3}}\right)+\left(\frac{\mathrm{97}−\mathrm{56}\sqrt{\mathrm{3}}}{\mathrm{9409}−\mathrm{9408}}\right) \\ $$$$=\mathrm{97}+\mathrm{97}=\:\mathrm{194} \\ $$$${and}\:{the}\:{same}\:{way} \\ $$$${x}=\mathrm{2}−\sqrt{\mathrm{3}}\:\Rightarrow{x}^{\mathrm{4}} +\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\:=\:\mathrm{194} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *