Question Number 13226 by chux last updated on 16/May/17
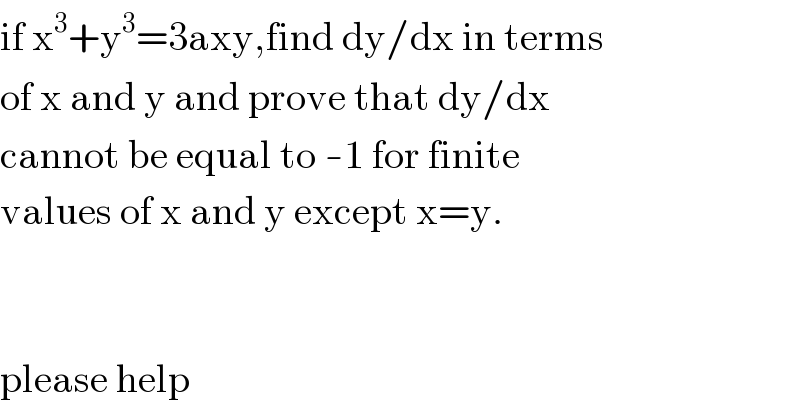
$$\mathrm{if}\:\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} =\mathrm{3axy},\mathrm{find}\:\mathrm{dy}/\mathrm{dx}\:\mathrm{in}\:\mathrm{terms} \\ $$$$\mathrm{of}\:\mathrm{x}\:\mathrm{and}\:\mathrm{y}\:\mathrm{and}\:\mathrm{prove}\:\mathrm{that}\:\mathrm{dy}/\mathrm{dx}\: \\ $$$$\mathrm{cannot}\:\mathrm{be}\:\mathrm{equal}\:\mathrm{to}\:-\mathrm{1}\:\mathrm{for}\:\mathrm{finite} \\ $$$$\mathrm{values}\:\mathrm{of}\:\mathrm{x}\:\mathrm{and}\:\mathrm{y}\:\mathrm{except}\:\mathrm{x}=\mathrm{y}. \\ $$$$ \\ $$$$ \\ $$$$\mathrm{please}\:\mathrm{help}\: \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 16/May/17
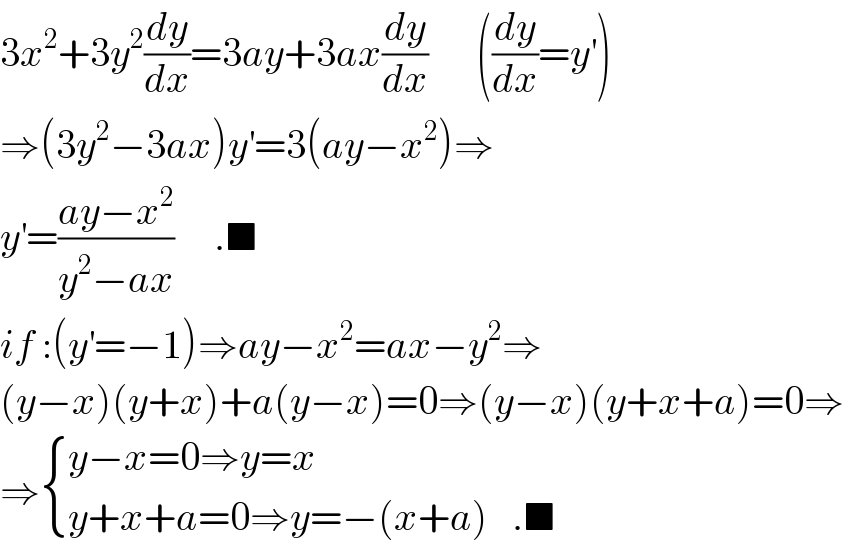
$$\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} \frac{{dy}}{{dx}}=\mathrm{3}{ay}+\mathrm{3}{ax}\frac{{dy}}{{dx}}\:\:\:\:\:\:\left(\frac{{dy}}{{dx}}={y}^{'} \right) \\ $$$$\Rightarrow\left(\mathrm{3}{y}^{\mathrm{2}} −\mathrm{3}{ax}\right){y}^{'} =\mathrm{3}\left({ay}−{x}^{\mathrm{2}} \right)\Rightarrow \\ $$$${y}^{'} =\frac{{ay}−{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} −{ax}}\:\:\:\:\:.\blacksquare \\ $$$${if}\::\left({y}^{'} =−\mathrm{1}\right)\Rightarrow{ay}−{x}^{\mathrm{2}} ={ax}−{y}^{\mathrm{2}} \Rightarrow \\ $$$$\left({y}−{x}\right)\left({y}+{x}\right)+{a}\left({y}−{x}\right)=\mathrm{0}\Rightarrow\left({y}−{x}\right)\left({y}+{x}+{a}\right)=\mathrm{0}\Rightarrow \\ $$$$\Rightarrow\begin{cases}{{y}−{x}=\mathrm{0}\Rightarrow{y}={x}}\\{{y}+{x}+{a}=\mathrm{0}\Rightarrow{y}=−\left({x}+{a}\right)\:\:\:.\blacksquare}\end{cases} \\ $$
Answered by ajfour last updated on 16/May/17
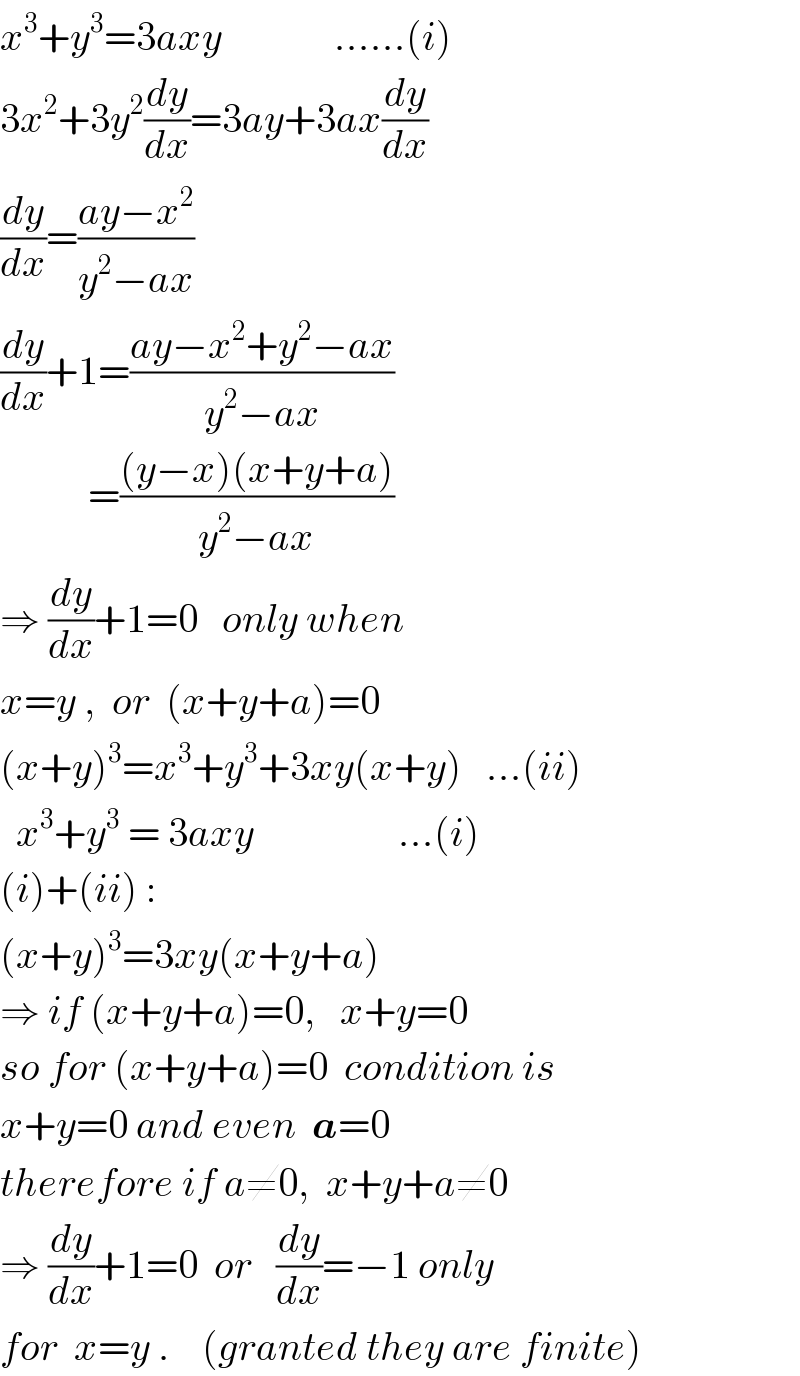
$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} =\mathrm{3}{axy}\:\:\:\:\:\:\:\:\:\:\:\:\:\:……\left({i}\right) \\ $$$$\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} \frac{{dy}}{{dx}}=\mathrm{3}{ay}+\mathrm{3}{ax}\frac{{dy}}{{dx}} \\ $$$$\frac{{dy}}{{dx}}=\frac{{ay}−{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} −{ax}} \\ $$$$\frac{{dy}}{{dx}}+\mathrm{1}=\frac{{ay}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −{ax}}{{y}^{\mathrm{2}} −{ax}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{\left({y}−{x}\right)\left({x}+{y}+{a}\right)}{{y}^{\mathrm{2}} −{ax}} \\ $$$$\Rightarrow\:\frac{{dy}}{{dx}}+\mathrm{1}=\mathrm{0}\:\:\:{only}\:{when}\: \\ $$$${x}={y}\:,\:\:{or}\:\:\left({x}+{y}+{a}\right)=\mathrm{0} \\ $$$$\left({x}+{y}\right)^{\mathrm{3}} ={x}^{\mathrm{3}} +{y}^{\mathrm{3}} +\mathrm{3}{xy}\left({x}+{y}\right)\:\:\:…\left({ii}\right) \\ $$$$\:\:{x}^{\mathrm{3}} +{y}^{\mathrm{3}} \:=\:\mathrm{3}{axy}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\left({i}\right) \\ $$$$\left({i}\right)+\left({ii}\right)\:: \\ $$$$\left({x}+{y}\right)^{\mathrm{3}} =\mathrm{3}{xy}\left({x}+{y}+{a}\right) \\ $$$$\Rightarrow\:{if}\:\left({x}+{y}+{a}\right)=\mathrm{0},\:\:\:{x}+{y}=\mathrm{0} \\ $$$${so}\:{for}\:\left({x}+{y}+{a}\right)=\mathrm{0}\:\:{condition}\:{is} \\ $$$${x}+{y}=\mathrm{0}\:{and}\:{even}\:\:\boldsymbol{{a}}=\mathrm{0}\: \\ $$$${therefore}\:{if}\:{a}\neq\mathrm{0},\:\:{x}+{y}+{a}\neq\mathrm{0} \\ $$$$\Rightarrow\:\frac{{dy}}{{dx}}+\mathrm{1}=\mathrm{0}\:\:{or}\:\:\:\frac{{dy}}{{dx}}=−\mathrm{1}\:{only} \\ $$$${for}\:\:{x}={y}\:.\:\:\:\:\left({granted}\:{they}\:{are}\:{finite}\right) \\ $$
Commented by chux last updated on 17/May/17

$$\mathrm{thanks}\:\mathrm{alot}. \\ $$
