Question Number 150979 by mathdanisur last updated on 17/Aug/21
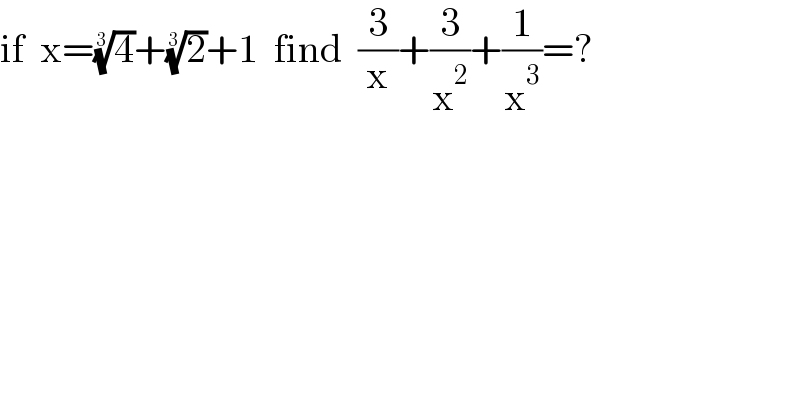
$$\mathrm{if}\:\:\mathrm{x}=\sqrt[{\mathrm{3}}]{\mathrm{4}}+\sqrt[{\mathrm{3}}]{\mathrm{2}}+\mathrm{1}\:\:\mathrm{find}\:\:\frac{\mathrm{3}}{\mathrm{x}}+\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }=? \\ $$$$ \\ $$
Answered by john_santu last updated on 18/Aug/21
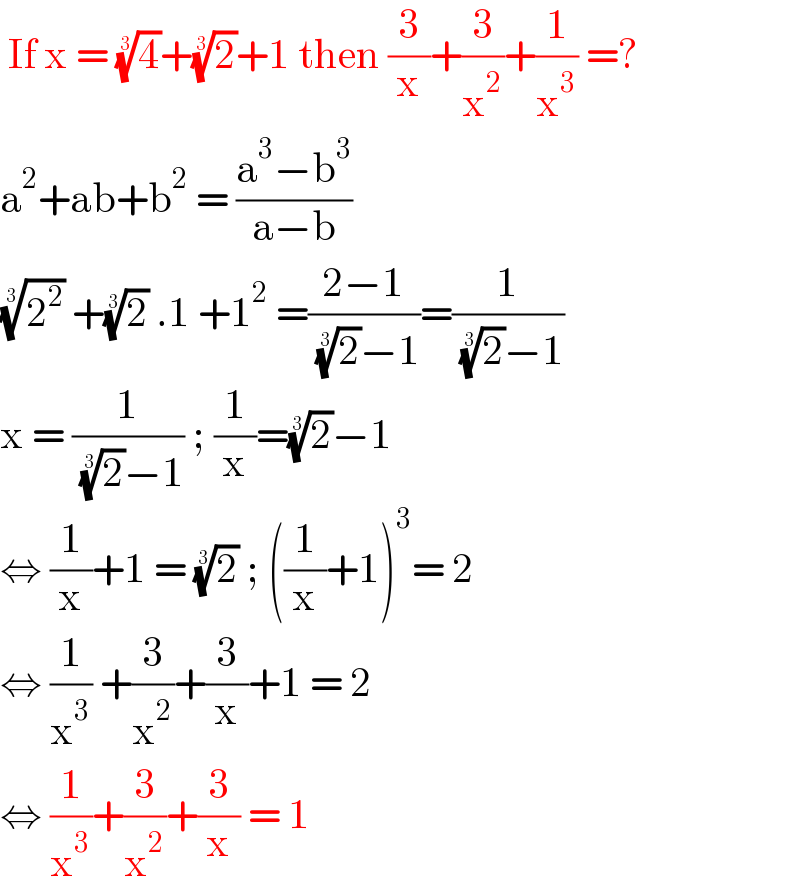
$$\:\mathrm{If}\:\mathrm{x}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{4}}+\sqrt[{\mathrm{3}}]{\mathrm{2}}+\mathrm{1}\:\mathrm{then}\:\frac{\mathrm{3}}{\mathrm{x}}+\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\:=? \\ $$$$\mathrm{a}^{\mathrm{2}} +\mathrm{ab}+\mathrm{b}^{\mathrm{2}} \:=\:\frac{\mathrm{a}^{\mathrm{3}} −\mathrm{b}^{\mathrm{3}} }{\mathrm{a}−\mathrm{b}}\: \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{2}^{\mathrm{2}} }\:+\sqrt[{\mathrm{3}}]{\mathrm{2}}\:.\mathrm{1}\:+\mathrm{1}^{\mathrm{2}} \:=\frac{\mathrm{2}−\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}}=\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}} \\ $$$$\mathrm{x}\:=\:\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}}\:;\:\frac{\mathrm{1}}{\mathrm{x}}=\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1} \\ $$$$\Leftrightarrow\:\frac{\mathrm{1}}{\mathrm{x}}+\mathrm{1}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{2}}\:;\:\left(\frac{\mathrm{1}}{\mathrm{x}}+\mathrm{1}\right)^{\mathrm{3}} =\:\mathrm{2} \\ $$$$\Leftrightarrow\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\:+\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{x}}+\mathrm{1}\:=\:\mathrm{2} \\ $$$$\Leftrightarrow\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }+\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{x}}\:=\:\mathrm{1}\: \\ $$
Commented by bramlexs22 last updated on 17/Aug/21
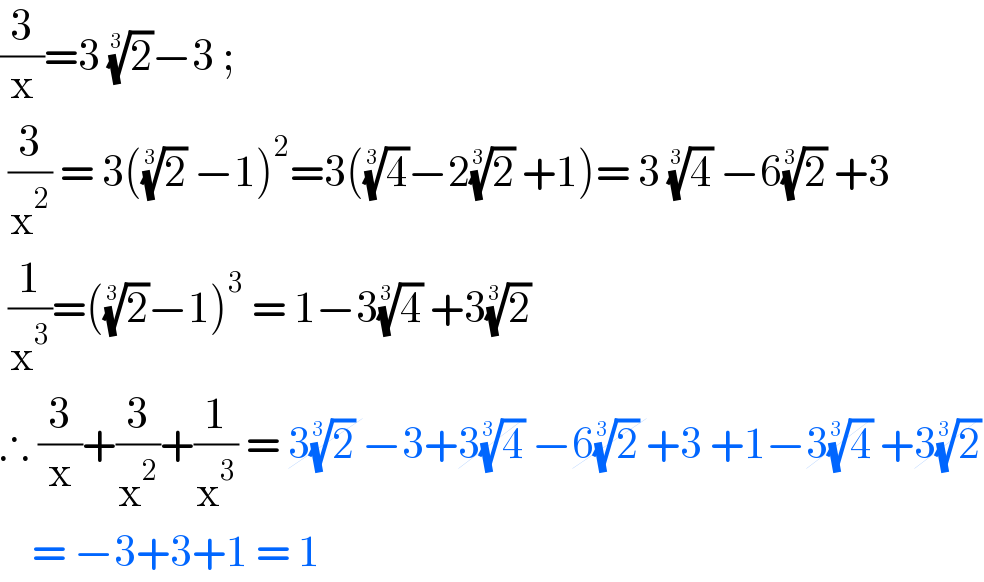
$$\frac{\mathrm{3}}{\mathrm{x}}=\mathrm{3}\:\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{3}\:; \\ $$$$\:\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{2}} }\:=\:\mathrm{3}\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}\:−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{3}\left(\sqrt[{\mathrm{3}}]{\mathrm{4}}−\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{2}}\:+\mathrm{1}\right)=\:\mathrm{3}\:\sqrt[{\mathrm{3}}]{\mathrm{4}}\:−\mathrm{6}\sqrt[{\mathrm{3}}]{\mathrm{2}}\:+\mathrm{3} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }=\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{3}} \:=\:\mathrm{1}−\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{4}}\:+\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{2}}\: \\ $$$$\therefore\:\frac{\mathrm{3}}{\mathrm{x}}+\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\:=\:\cancel{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{2}}\:}−\mathrm{3}+\cancel{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{4}}}\:−\cancel{\mathrm{6}\sqrt[{\mathrm{3}}]{\mathrm{2}}\:}+\mathrm{3}\:+\mathrm{1}−\cancel{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{4}}}\:+\cancel{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{2}}} \\ $$$$\:\:\:\:=\:−\mathrm{3}+\mathrm{3}+\mathrm{1}\:=\:\mathrm{1} \\ $$
Commented by mathdanisur last updated on 17/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser} \\ $$
