Question Number 144839 by mathdanisur last updated on 29/Jun/21
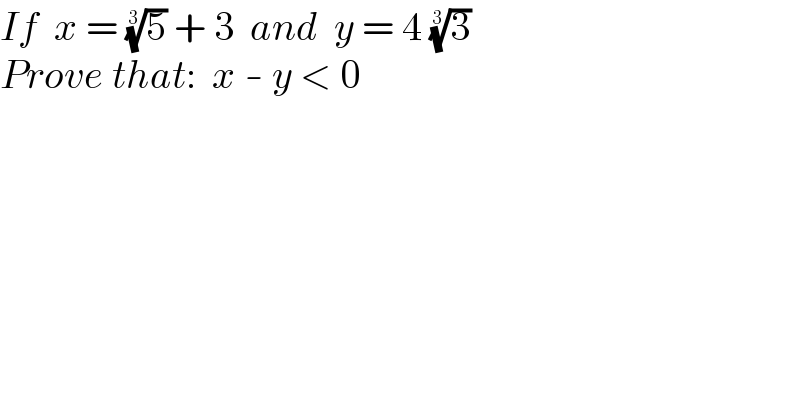
$${If}\:\:{x}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{5}}\:+\:\mathrm{3}\:\:{and}\:\:{y}\:=\:\mathrm{4}\:\sqrt[{\mathrm{3}}]{\mathrm{3}} \\ $$$${Prove}\:{that}:\:\:{x}\:-\:{y}\:<\:\mathrm{0} \\ $$
Answered by ajfour last updated on 29/Jun/21
![(x−3)^3 =5 y^3 =192 ...(i) x^3 −9x^2 +27x−27=5 ...(ii) subtracting ..(i) from (ii) (x−y){[(x−y)+((3y)/2)]^2 +((3y^2 )/4)} +9x^2 +27x+160=0 for x>0, above eq. is true only if x−y<0 ; (and above eq. is of course true).](https://www.tinkutara.com/question/Q144847.png)
$$\left({x}−\mathrm{3}\right)^{\mathrm{3}} =\mathrm{5} \\ $$$${y}^{\mathrm{3}} =\mathrm{192}\:\:\:…\left({i}\right) \\ $$$${x}^{\mathrm{3}} −\mathrm{9}{x}^{\mathrm{2}} +\mathrm{27}{x}−\mathrm{27}=\mathrm{5}\:\:\:…\left({ii}\right) \\ $$$${subtracting}\:\:..\left({i}\right)\:\:{from}\:\left({ii}\right) \\ $$$$\left({x}−{y}\right)\left\{\left[\left({x}−{y}\right)+\frac{\mathrm{3}{y}}{\mathrm{2}}\right]^{\mathrm{2}} +\frac{\mathrm{3}{y}^{\mathrm{2}} }{\mathrm{4}}\right\} \\ $$$$+\mathrm{9}{x}^{\mathrm{2}} +\mathrm{27}{x}+\mathrm{160}=\mathrm{0} \\ $$$${for}\:{x}>\mathrm{0},\:\:\:{above}\:{eq}.\:{is}\:{true} \\ $$$${only}\:{if}\:\:{x}−{y}<\mathrm{0}\:;\:\left({and}\:{above}\right. \\ $$$$\left.{eq}.\:{is}\:{of}\:{course}\:{true}\right). \\ $$
Commented by mathdanisur last updated on 29/Jun/21
$${thankyou}\:{Sir}\:{cool} \\ $$
Answered by Rakshay last updated on 29/Jun/21

$${suppose}\:{x}−{y}\geqslant\mathrm{0} \\ $$$${i}.{e}\:\:\:\:\:\:\:^{\mathrm{3}} \sqrt{\mathrm{5}}+\mathrm{3}−\mathrm{4}\:^{\mathrm{3}} \sqrt{\mathrm{3}}\geqslant\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\Rightarrow\mathrm{4}\:^{\mathrm{3}} \sqrt{\mathrm{3}}−^{\mathrm{3}} \sqrt{\mathrm{5}}\leqslant\mathrm{3}…..\left(\mathrm{1}\right) \\ $$$$\Rightarrow\:\:\left(\mathrm{4}\:^{\mathrm{3}} \sqrt{\mathrm{3}}−^{\mathrm{3}} \sqrt{\mathrm{5}}\right)^{\mathrm{3}} \leqslant\mathrm{27} \\ $$$$\:\:\:\left(\mathrm{64}\right)\left(\mathrm{3}\right)−\left(\mathrm{5}\right)−\mathrm{3}\left(\mathrm{4}\:\right)\left(^{\mathrm{3}} \sqrt{\mathrm{15}}\right)\left(\mathrm{4}\:^{\mathrm{3}} \sqrt{\mathrm{3}}−^{\mathrm{3}} \sqrt{\mathrm{5}}\right)\leqslant\mathrm{27} \\ $$$$\mathrm{204}−\mathrm{5}−\mathrm{12}\left(^{\mathrm{3}} \sqrt{\mathrm{15}}\right)\left(\mathrm{4}\:^{\mathrm{3}} \sqrt{\mathrm{3}}\:−^{\mathrm{3}} \sqrt{\mathrm{5}}\right)\leqslant\mathrm{27} \\ $$$$\Rightarrow\mathrm{172}−\mathrm{12}\left(^{\mathrm{3}} \sqrt{\mathrm{15}}\right)\left(\mathrm{4}\:^{\mathrm{3}} \sqrt{\mathrm{3}}−^{\mathrm{3}} \sqrt{\mathrm{5}}\right)\leqslant\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{172}}{\mathrm{12}}\leqslant\left(^{\mathrm{3}} \sqrt{\mathrm{15}}\right)\left(\mathrm{4}\:^{\mathrm{3}} \sqrt{\mathrm{3}}−^{\mathrm{3}} \sqrt{\mathrm{5}}\right)\leqslant\left(\mathrm{3}\right)\left(^{\mathrm{3}} \sqrt{\mathrm{15}}\right) \\ $$$$\Rightarrow\frac{\mathrm{172}}{\mathrm{36}}\leqslant^{\mathrm{3}} \sqrt{\mathrm{15}}\left(\:{which}\:{isn}'{t}\:{true}\right)\: \\ $$$${so}\:{our}\:{supposition}\:{is}\:{wrong},\:{thus}, \\ $$$${x}−{y}<\mathrm{0} \\ $$
Commented by mathdanisur last updated on 29/Jun/21

$${thanks}\:{Sir}\:{cool} \\ $$
Answered by mr W last updated on 29/Jun/21
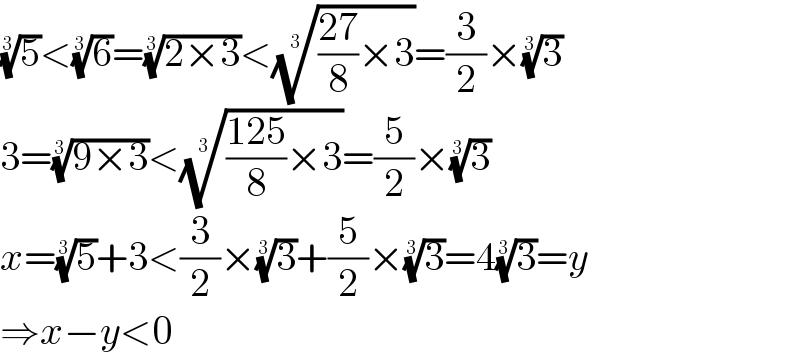
$$\sqrt[{\mathrm{3}}]{\mathrm{5}}<\sqrt[{\mathrm{3}}]{\mathrm{6}}=\sqrt[{\mathrm{3}}]{\mathrm{2}×\mathrm{3}}<\sqrt[{\mathrm{3}}]{\frac{\mathrm{27}}{\mathrm{8}}×\mathrm{3}}=\frac{\mathrm{3}}{\mathrm{2}}×\sqrt[{\mathrm{3}}]{\mathrm{3}} \\ $$$$\mathrm{3}=\sqrt[{\mathrm{3}}]{\mathrm{9}×\mathrm{3}}<\sqrt[{\mathrm{3}}]{\frac{\mathrm{125}}{\mathrm{8}}×\mathrm{3}}=\frac{\mathrm{5}}{\mathrm{2}}×\sqrt[{\mathrm{3}}]{\mathrm{3}} \\ $$$${x}=\sqrt[{\mathrm{3}}]{\mathrm{5}}+\mathrm{3}<\frac{\mathrm{3}}{\mathrm{2}}×\sqrt[{\mathrm{3}}]{\mathrm{3}}+\frac{\mathrm{5}}{\mathrm{2}}×\sqrt[{\mathrm{3}}]{\mathrm{3}}=\mathrm{4}\sqrt[{\mathrm{3}}]{\mathrm{3}}={y} \\ $$$$\Rightarrow{x}−{y}<\mathrm{0} \\ $$
Commented by mathdanisur last updated on 29/Jun/21

$${cool}\:{Sir}\:{thanks} \\ $$
