Menu Close

if-x-6-y-6-9-x-4-y-4-5-then-x-2-y-2-

Tinku Tara 0 Comments
Pin




Question Number 175373 by infinityaction last updated on 28/Aug/22
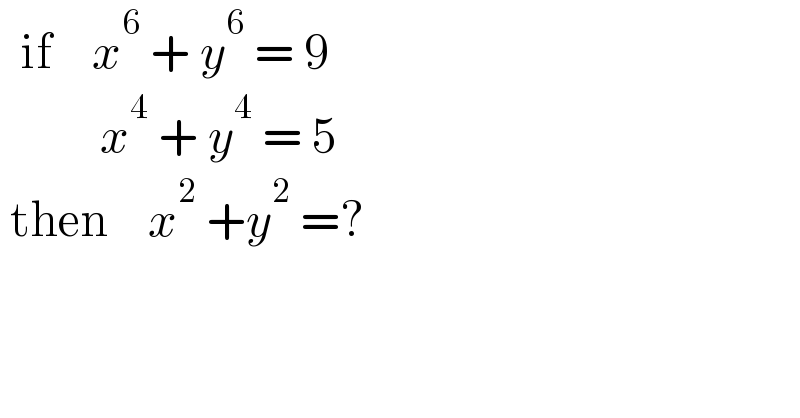
if x^6 + y^6 = 9 x^4 + y^4 = 5 then x^2 +y^2 =?
$$\:\:\mathrm{if}\:\:\:\:{x}^{\mathrm{6}} \:+\:{y}^{\mathrm{6}} \:=\:\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{4}} \:+\:{y}^{\mathrm{4}} \:=\:\mathrm{5} \\ $$$$\:\mathrm{then}\:\:\:\:{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:=? \\ $$
Answered by mr W last updated on 28/Aug/22
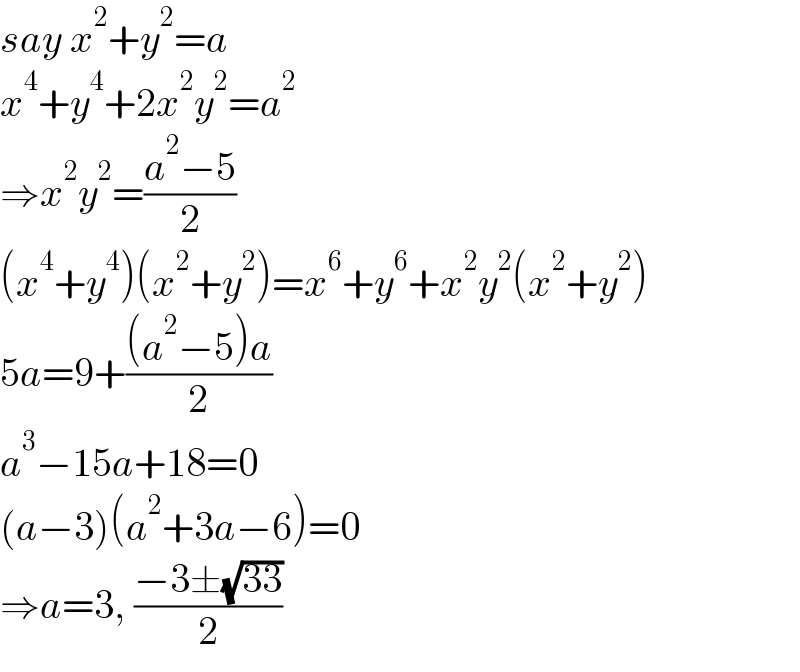
say x^2 +y^2 =a x^4 +y^4 +2x^2 y^2 =a^2 ⇒x^2 y^2 =((a^2 −5)/2) (x^4 +y^4 )(x^2 +y^2 )=x^6 +y^6 +x^2 y^2 (x^2 +y^2 ) 5a=9+(((a^2 −5)a)/2) a^3 −15a+18=0 (a−3)(a^2 +3a−6)=0 ⇒a=3, ((−3±(√(33)))/2)
$${say}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={a} \\ $$$${x}^{\mathrm{4}} +{y}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} {y}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} −\mathrm{5}}{\mathrm{2}} \\ $$$$\left({x}^{\mathrm{4}} +{y}^{\mathrm{4}} \right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)={x}^{\mathrm{6}} +{y}^{\mathrm{6}} +{x}^{\mathrm{2}} {y}^{\mathrm{2}} \left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right) \\ $$$$\mathrm{5}{a}=\mathrm{9}+\frac{\left({a}^{\mathrm{2}} −\mathrm{5}\right){a}}{\mathrm{2}} \\ $$$${a}^{\mathrm{3}} −\mathrm{15}{a}+\mathrm{18}=\mathrm{0} \\ $$$$\left({a}−\mathrm{3}\right)\left({a}^{\mathrm{2}} +\mathrm{3}{a}−\mathrm{6}\right)=\mathrm{0} \\ $$$$\Rightarrow{a}=\mathrm{3},\:\frac{−\mathrm{3}\pm\sqrt{\mathrm{33}}}{\mathrm{2}} \\ $$
Commented by Tawa11 last updated on 28/Aug/22
Great sirs
$$\mathrm{Great}\:\mathrm{sirs} \\ $$
Answered by Rasheed.Sindhi last updated on 28/Aug/22
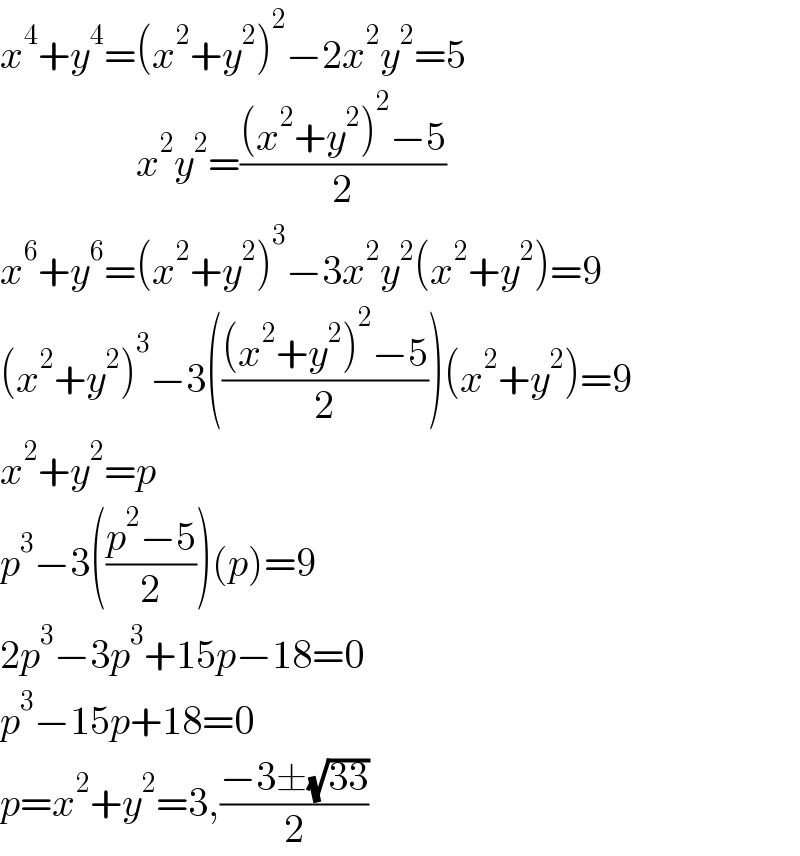
x^4 +y^4 =(x^2 +y^2 )^2 −2x^2 y^2 =5 x^2 y^2 =(((x^2 +y^2 )^2 −5)/2) x^6 +y^6 =(x^2 +y^2 )^3 −3x^2 y^2 (x^2 +y^2 )=9 (x^2 +y^2 )^3 −3((((x^2 +y^2 )^2 −5)/2))(x^2 +y^2 )=9 x^2 +y^2 =p p^3 −3(((p^2 −5)/2))(p)=9 2p^3 −3p^3 +15p−18=0 p^3 −15p+18=0 p=x^2 +y^2 =3,((−3±(√(33)))/2)
$${x}^{\mathrm{4}} +{y}^{\mathrm{4}} =\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} =\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} {y}^{\mathrm{2}} =\frac{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{5}}{\mathrm{2}} \\ $$$${x}^{\mathrm{6}} +{y}^{\mathrm{6}} =\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)=\mathrm{9} \\ $$$$\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{3}} −\mathrm{3}\left(\frac{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{5}}{\mathrm{2}}\right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)=\mathrm{9} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={p}\: \\ $$$${p}^{\mathrm{3}} −\mathrm{3}\left(\frac{{p}^{\mathrm{2}} −\mathrm{5}}{\mathrm{2}}\right)\left({p}\right)=\mathrm{9} \\ $$$$\mathrm{2}{p}^{\mathrm{3}} −\mathrm{3}{p}^{\mathrm{3}} +\mathrm{15}{p}−\mathrm{18}=\mathrm{0} \\ $$$${p}^{\mathrm{3}} −\mathrm{15}{p}+\mathrm{18}=\mathrm{0} \\ $$$${p}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{3},\frac{−\mathrm{3}\pm\sqrt{\mathrm{33}}}{\mathrm{2}} \\ $$
Answered by Rasheed.Sindhi last updated on 28/Aug/22
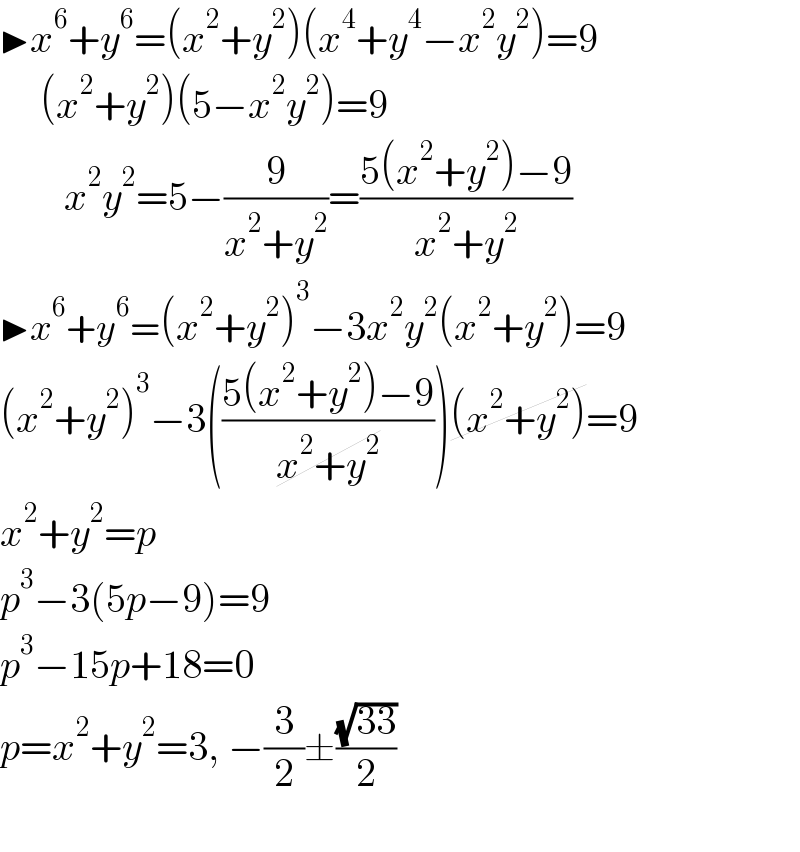
▶x^6 +y^6 =(x^2 +y^2 )(x^4 +y^4 −x^2 y^2 )=9 (x^2 +y^2 )(5−x^2 y^2 )=9 x^2 y^2 =5−(9/(x^2 +y^2 ))=((5(x^2 +y^2 )−9)/(x^2 +y^2 )) ▶x^6 +y^6 =(x^2 +y^2 )^3 −3x^2 y^2 (x^2 +y^2 )=9 (x^2 +y^2 )^3 −3(((5(x^2 +y^2 )−9)/(x^2 +y^2 )))(x^2 +y^2 )=9 x^2 +y^2 =p p^3 −3(5p−9)=9 p^3 −15p+18=0 p=x^2 +y^2 =3, −(3/2)±((√(33))/2)
$$\blacktriangleright{x}^{\mathrm{6}} +{y}^{\mathrm{6}} =\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\left({x}^{\mathrm{4}} +{y}^{\mathrm{4}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} \right)=\mathrm{9} \\ $$$$\:\:\:\:\:\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\left(\mathrm{5}−{x}^{\mathrm{2}} {y}^{\mathrm{2}} \right)=\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} {y}^{\mathrm{2}} =\mathrm{5}−\frac{\mathrm{9}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }=\frac{\mathrm{5}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)−\mathrm{9}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$\blacktriangleright{x}^{\mathrm{6}} +{y}^{\mathrm{6}} =\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)=\mathrm{9} \\ $$$$\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{3}} −\mathrm{3}\left(\frac{\mathrm{5}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)−\mathrm{9}}{\cancel{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}\right)\cancel{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)}=\mathrm{9} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={p} \\ $$$${p}^{\mathrm{3}} −\mathrm{3}\left(\mathrm{5}{p}−\mathrm{9}\right)=\mathrm{9} \\ $$$${p}^{\mathrm{3}} −\mathrm{15}{p}+\mathrm{18}=\mathrm{0} \\ $$$${p}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{3},\:−\frac{\mathrm{3}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{33}}}{\mathrm{2}} \\ $$$$ \\ $$
Commented by infinityaction last updated on 28/Aug/22
thanks
$${thanks}\: \\ $$
Answered by ajfour last updated on 29/Aug/22
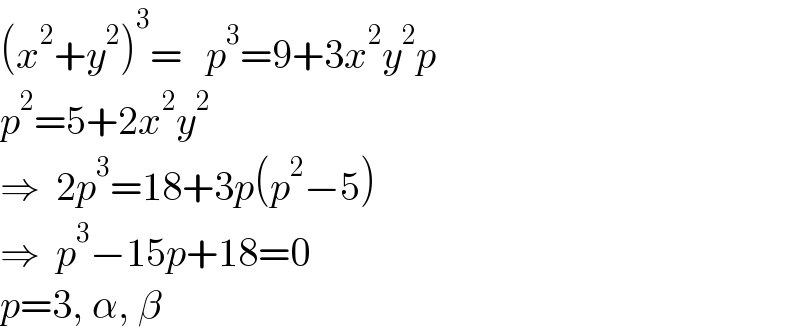
(x^2 +y^2 )^3 = p^3 =9+3x^2 y^2 p p^2 =5+2x^2 y^2 ⇒ 2p^3 =18+3p(p^2 −5) ⇒ p^3 −15p+18=0 p=3, α, β
$$\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{3}} =\:\:\:{p}^{\mathrm{3}} =\mathrm{9}+\mathrm{3}{x}^{\mathrm{2}} {y}^{\mathrm{2}} {p} \\ $$$${p}^{\mathrm{2}} =\mathrm{5}+\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{2}{p}^{\mathrm{3}} =\mathrm{18}+\mathrm{3}{p}\left({p}^{\mathrm{2}} −\mathrm{5}\right) \\ $$$$\Rightarrow\:\:{p}^{\mathrm{3}} −\mathrm{15}{p}+\mathrm{18}=\mathrm{0} \\ $$$${p}=\mathrm{3},\:\alpha,\:\beta \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *