Question Number 154973 by mathdanisur last updated on 23/Sep/21

$$\mathrm{If}\:\:\mathrm{x}\:+\:\frac{\mathrm{7}}{\:\sqrt{\mathrm{x}}}\:=\:\mathrm{50} \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{the}\:\mathrm{expression} \\ $$$$\sqrt{\mathrm{x}}\:-\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}}}\:=\:? \\ $$
Answered by mr W last updated on 23/Sep/21
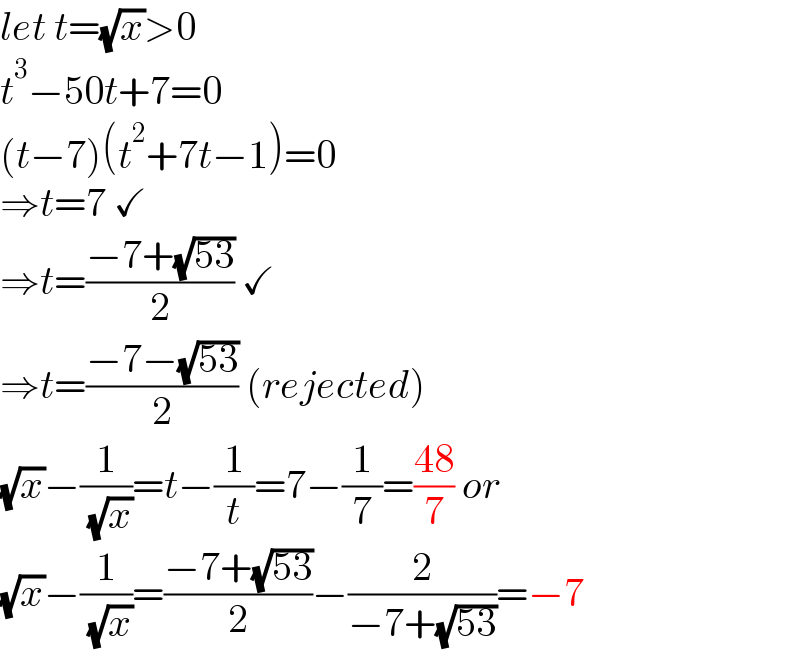
$${let}\:{t}=\sqrt{{x}}>\mathrm{0} \\ $$$${t}^{\mathrm{3}} −\mathrm{50}{t}+\mathrm{7}=\mathrm{0} \\ $$$$\left({t}−\mathrm{7}\right)\left({t}^{\mathrm{2}} +\mathrm{7}{t}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{t}=\mathrm{7}\:\checkmark \\ $$$$\Rightarrow{t}=\frac{−\mathrm{7}+\sqrt{\mathrm{53}}}{\mathrm{2}}\:\checkmark \\ $$$$\Rightarrow{t}=\frac{−\mathrm{7}−\sqrt{\mathrm{53}}}{\mathrm{2}}\:\left({rejected}\right) \\ $$$$\sqrt{{x}}−\frac{\mathrm{1}}{\:\sqrt{{x}}}={t}−\frac{\mathrm{1}}{{t}}=\mathrm{7}−\frac{\mathrm{1}}{\mathrm{7}}=\frac{\mathrm{48}}{\mathrm{7}}\:{or} \\ $$$$\sqrt{{x}}−\frac{\mathrm{1}}{\:\sqrt{{x}}}=\frac{−\mathrm{7}+\sqrt{\mathrm{53}}}{\mathrm{2}}−\frac{\mathrm{2}}{−\mathrm{7}+\sqrt{\mathrm{53}}}=−\mathrm{7} \\ $$
Commented by mathdanisur last updated on 23/Sep/21
$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{solution},\:\boldsymbol{\mathrm{S}}\mathrm{er}\:\mathrm{thankyou} \\ $$
