if-x-a-integer-number-when-divided-8-has-remainder-5-and-divided-5-has-remainder-2-find-x-

Question Number 101891 by bobhans last updated on 05/Jul/20

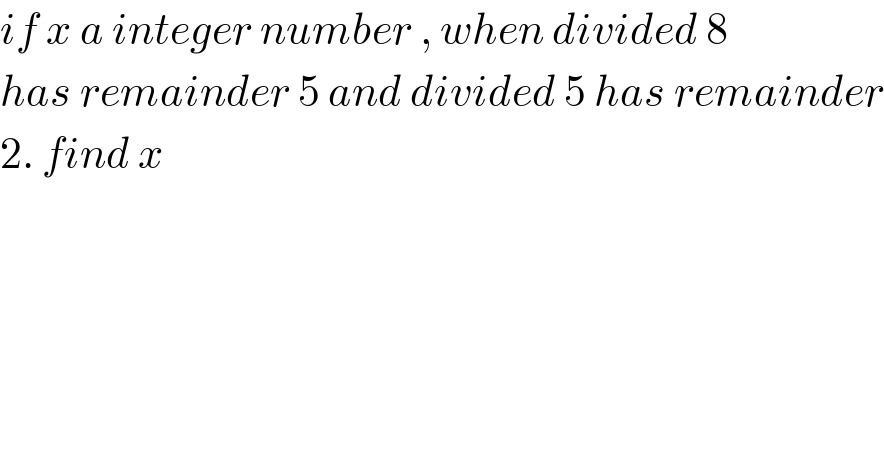
$${if}\:{x}\:{a}\:{integer}\:{number}\:,\:{when}\:{divided}\:\mathrm{8} \\ $$$${has}\:{remainder}\:\mathrm{5}\:{and}\:{divided}\:\mathrm{5}\:{has}\:{remainder} \\ $$$$\mathrm{2}.\:{find}\:{x} \\ $$

Answered by Rasheed.Sindhi last updated on 05/Jul/20

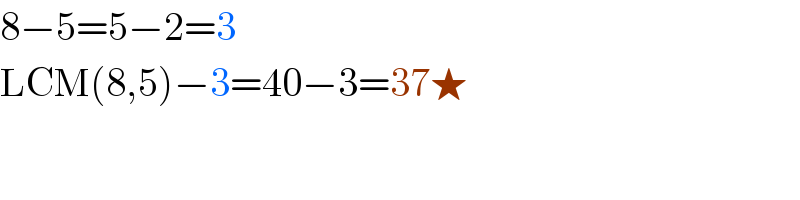
$$\mathrm{8}−\mathrm{5}=\mathrm{5}−\mathrm{2}=\mathrm{3} \\ $$$$\mathrm{LCM}\left(\mathrm{8},\mathrm{5}\right)−\mathrm{3}=\mathrm{40}−\mathrm{3}=\mathrm{37}\bigstar \\ $$

Commented by Rasheed.Sindhi last updated on 05/Jul/20

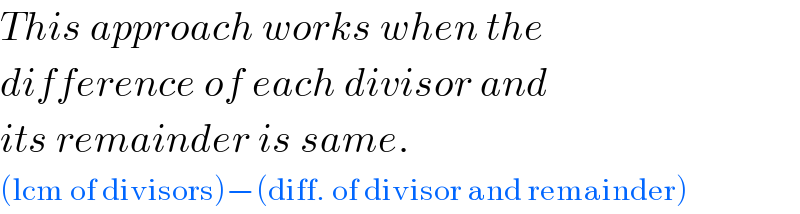
This approach works when the difference of each divisor and its remainder is same. (lcm of divisors)−(diff. of divisor and remainder)

$${This}\:{approach}\:{works}\:{when}\:{the} \\ $$$${difference}\:{of}\:{each}\:{divisor}\:{and} \\ $$$${its}\:{remainder}\:{is}\:{same}. \\ $$$$\left(\mathrm{lcm}\:\mathrm{of}\:\mathrm{divisors}\right)−\left(\mathrm{diff}.\:\mathrm{of}\:\mathrm{divisor}\:\mathrm{and}\:\mathrm{remainder}\right) \\ $$

Commented by bemath last updated on 06/Jul/20

$${great}\:{sir} \\ $$

Answered by john santu last updated on 05/Jul/20

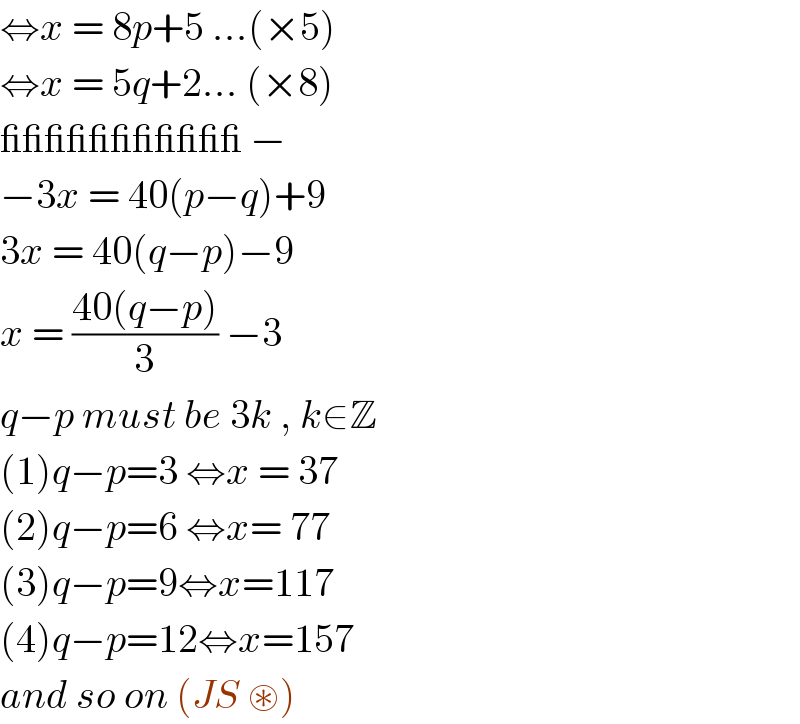
⇔x = 8p+5 ...(×5) ⇔x = 5q+2... (×8) ___________ − −3x = 40(p−q)+9 3x = 40(q−p)−9 x = ((40(q−p))/3) −3 q−p must be 3k , k∈Z (1)q−p=3 ⇔x = 37 (2)q−p=6 ⇔x= 77 (3)q−p=9⇔x=117 (4)q−p=12⇔x=157 and so on (JS ⊛)

$$\Leftrightarrow{x}\:=\:\mathrm{8}{p}+\mathrm{5}\:…\left(×\mathrm{5}\right) \\ $$$$\Leftrightarrow{x}\:=\:\mathrm{5}{q}+\mathrm{2}…\:\left(×\mathrm{8}\right) \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\:− \\ $$$$−\mathrm{3}{x}\:=\:\mathrm{40}\left({p}−{q}\right)+\mathrm{9} \\ $$$$\mathrm{3}{x}\:=\:\mathrm{40}\left({q}−{p}\right)−\mathrm{9} \\ $$$${x}\:=\:\frac{\mathrm{40}\left({q}−{p}\right)}{\mathrm{3}}\:−\mathrm{3}\: \\ $$$${q}−{p}\:{must}\:{be}\:\mathrm{3}{k}\:,\:{k}\in\mathbb{Z} \\ $$$$\left(\mathrm{1}\right){q}−{p}=\mathrm{3}\:\Leftrightarrow{x}\:=\:\mathrm{37} \\ $$$$\left(\mathrm{2}\right){q}−{p}=\mathrm{6}\:\Leftrightarrow{x}=\:\mathrm{77} \\ $$$$\left(\mathrm{3}\right){q}−{p}=\mathrm{9}\Leftrightarrow{x}=\mathrm{117} \\ $$$$\left(\mathrm{4}\right){q}−{p}=\mathrm{12}\Leftrightarrow{x}=\mathrm{157} \\ $$$${and}\:{so}\:{on}\:\left({JS}\:\circledast\right)\: \\ $$

Answered by floor(10²Eta[1]) last updated on 22/Jul/20

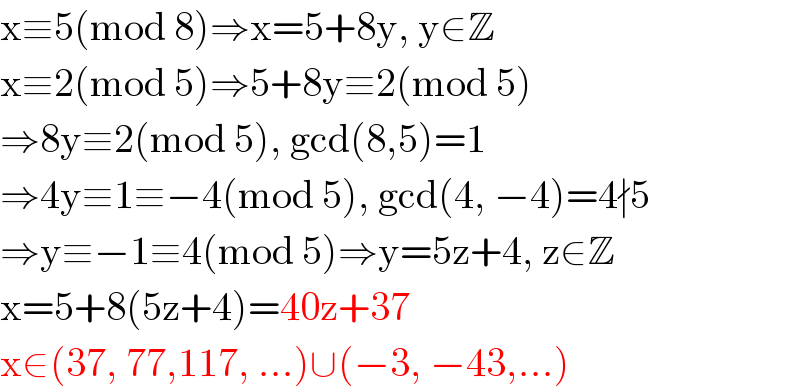
x≡5(mod 8)⇒x=5+8y, y∈Z x≡2(mod 5)⇒5+8y≡2(mod 5) ⇒8y≡2(mod 5), gcd(8,5)=1 ⇒4y≡1≡−4(mod 5), gcd(4, −4)=4∤5 ⇒y≡−1≡4(mod 5)⇒y=5z+4, z∈Z x=5+8(5z+4)=40z+37 x∈(37, 77,117, ...)∪(−3, −43,...)

$$\mathrm{x}\equiv\mathrm{5}\left(\mathrm{mod}\:\mathrm{8}\right)\Rightarrow\mathrm{x}=\mathrm{5}+\mathrm{8y},\:\mathrm{y}\in\mathbb{Z} \\ $$$$\mathrm{x}\equiv\mathrm{2}\left(\mathrm{mod}\:\mathrm{5}\right)\Rightarrow\mathrm{5}+\mathrm{8y}\equiv\mathrm{2}\left(\mathrm{mod}\:\mathrm{5}\right) \\ $$$$\Rightarrow\mathrm{8y}\equiv\mathrm{2}\left(\mathrm{mod}\:\mathrm{5}\right),\:\mathrm{gcd}\left(\mathrm{8},\mathrm{5}\right)=\mathrm{1} \\ $$$$\Rightarrow\mathrm{4y}\equiv\mathrm{1}\equiv−\mathrm{4}\left(\mathrm{mod}\:\mathrm{5}\right),\:\mathrm{gcd}\left(\mathrm{4},\:−\mathrm{4}\right)=\mathrm{4}\nmid\mathrm{5} \\ $$$$\Rightarrow\mathrm{y}\equiv−\mathrm{1}\equiv\mathrm{4}\left(\mathrm{mod}\:\mathrm{5}\right)\Rightarrow\mathrm{y}=\mathrm{5z}+\mathrm{4},\:\mathrm{z}\in\mathbb{Z} \\ $$$$\mathrm{x}=\mathrm{5}+\mathrm{8}\left(\mathrm{5z}+\mathrm{4}\right)=\mathrm{40z}+\mathrm{37} \\ $$$$\mathrm{x}\in\left(\mathrm{37},\:\mathrm{77},\mathrm{117},\:…\right)\cup\left(−\mathrm{3},\:−\mathrm{43},…\right) \\ $$

Facebook Tweet Pin

if-x-a-integer-number-when-divided-8-has-remainder-5-and-divided-5-has-remainder-2-find-x-

Leave a Reply Cancel reply