Question Number 158444 by HongKing last updated on 04/Nov/21

Commented by mr W last updated on 04/Nov/21

Commented by HongKing last updated on 04/Nov/21
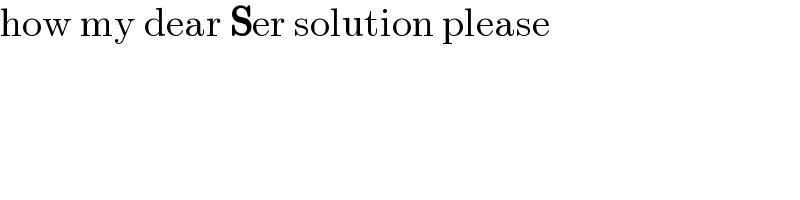
Commented by Rasheed.Sindhi last updated on 04/Nov/21

Commented by mr W last updated on 04/Nov/21
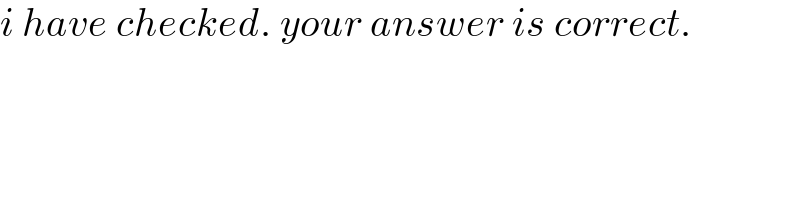
Commented by Rasheed.Sindhi last updated on 05/Nov/21
Answered by mr W last updated on 04/Nov/21
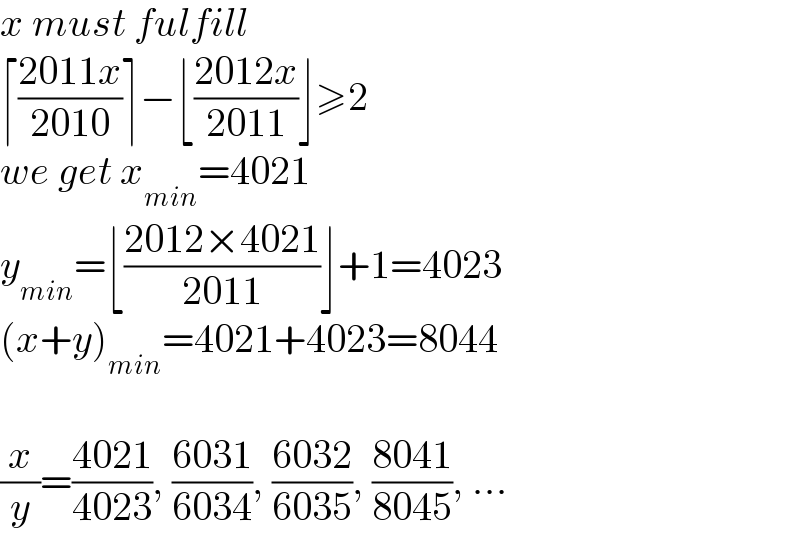
Commented by Rasheed.Sindhi last updated on 06/Nov/21
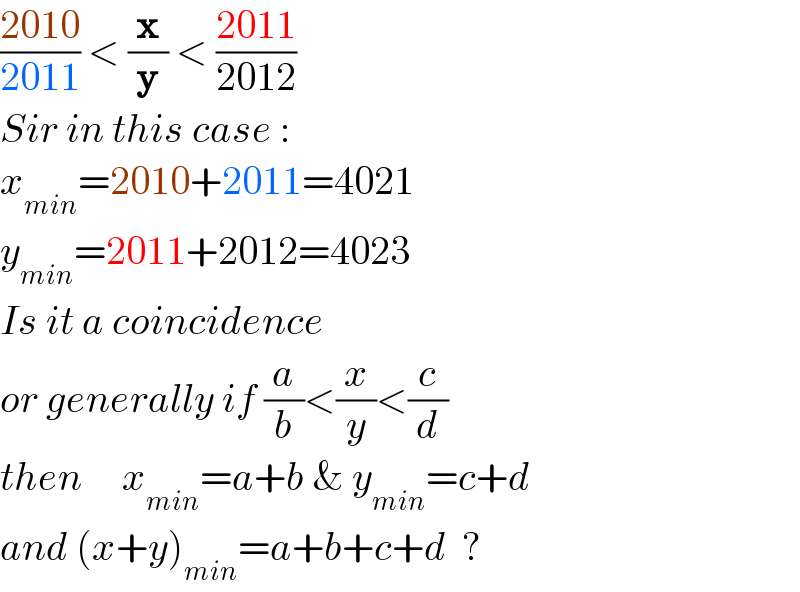
Commented by mr W last updated on 06/Nov/21
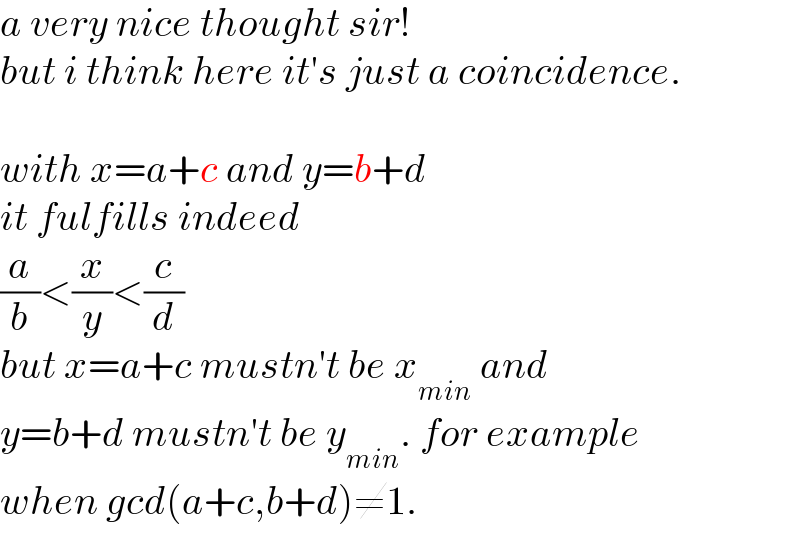
Commented by mr W last updated on 06/Nov/21

Commented by Rasheed.Sindhi last updated on 06/Nov/21
ㄒ卄卂几Ҝ丂 爪尺 山 丂丨尺!
