Question Number 128808 by liberty last updated on 10/Jan/21
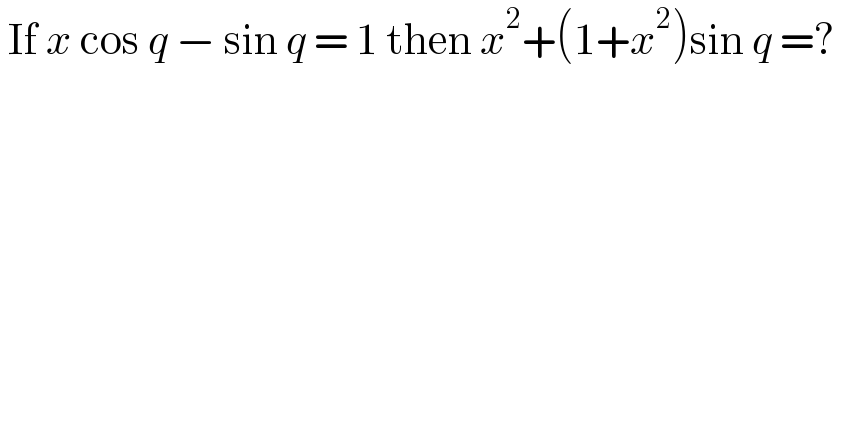
$$\:\mathrm{If}\:{x}\:\mathrm{cos}\:{q}\:−\:\mathrm{sin}\:{q}\:=\:\mathrm{1}\:\mathrm{then}\:{x}^{\mathrm{2}} +\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\mathrm{sin}\:{q}\:=?\: \\ $$
Commented by benjo_mathlover last updated on 10/Jan/21
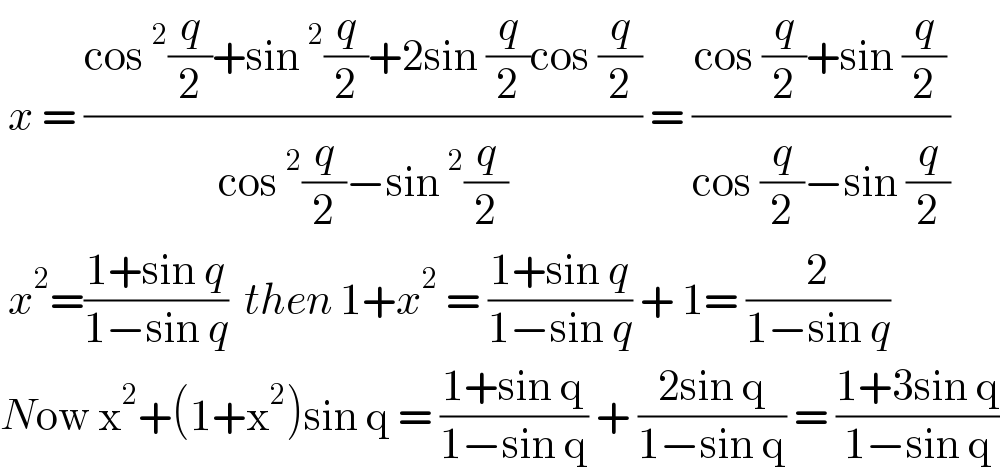
$$\:{x}\:=\:\frac{\mathrm{cos}\:^{\mathrm{2}} \frac{{q}}{\mathrm{2}}+\mathrm{sin}\:^{\mathrm{2}} \frac{{q}}{\mathrm{2}}+\mathrm{2sin}\:\frac{{q}}{\mathrm{2}}\mathrm{cos}\:\frac{{q}}{\mathrm{2}}}{\mathrm{cos}\:^{\mathrm{2}} \frac{{q}}{\mathrm{2}}−\mathrm{sin}\:^{\mathrm{2}} \frac{{q}}{\mathrm{2}}}\:=\:\frac{\mathrm{cos}\:\frac{{q}}{\mathrm{2}}+\mathrm{sin}\:\frac{{q}}{\mathrm{2}}}{\mathrm{cos}\:\frac{{q}}{\mathrm{2}}−\mathrm{sin}\:\frac{{q}}{\mathrm{2}}} \\ $$$$\:{x}^{\mathrm{2}} =\frac{\mathrm{1}+\mathrm{sin}\:{q}}{\mathrm{1}−\mathrm{sin}\:{q}}\:\:{then}\:\mathrm{1}+{x}^{\mathrm{2}} \:=\:\frac{\mathrm{1}+\mathrm{sin}\:{q}}{\mathrm{1}−\mathrm{sin}\:{q}}\:+\:\mathrm{1}=\:\frac{\mathrm{2}}{\mathrm{1}−\mathrm{sin}\:{q}} \\ $$$${N}\mathrm{ow}\:\mathrm{x}^{\mathrm{2}} +\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{sin}\:\mathrm{q}\:=\:\frac{\mathrm{1}+\mathrm{sin}\:\mathrm{q}}{\mathrm{1}−\mathrm{sin}\:\mathrm{q}}\:+\:\frac{\mathrm{2sin}\:\mathrm{q}}{\mathrm{1}−\mathrm{sin}\:\mathrm{q}}\:=\:\frac{\mathrm{1}+\mathrm{3sin}\:\mathrm{q}}{\mathrm{1}−\mathrm{sin}\:\mathrm{q}} \\ $$
Answered by bramlexs22 last updated on 10/Jan/21
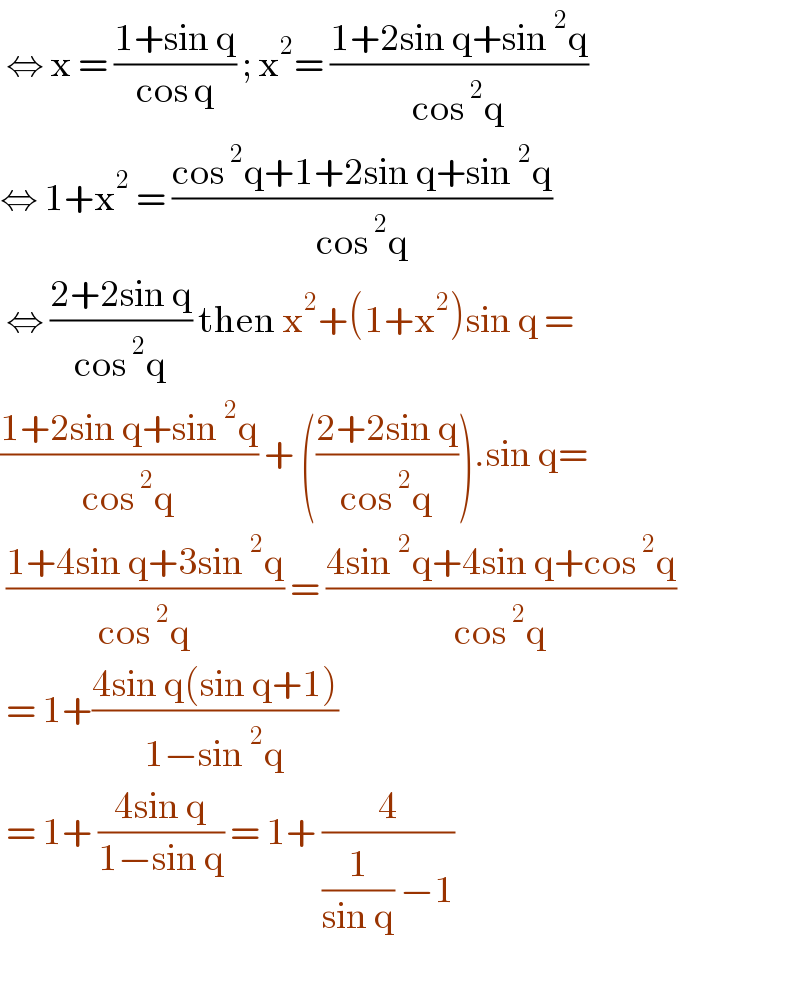
$$\:\Leftrightarrow\:\mathrm{x}\:=\:\frac{\mathrm{1}+\mathrm{sin}\:\mathrm{q}}{\mathrm{cos}\:\mathrm{q}}\:;\:\mathrm{x}^{\mathrm{2}} =\:\frac{\mathrm{1}+\mathrm{2sin}\:\mathrm{q}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{q}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{q}} \\ $$$$\Leftrightarrow\:\mathrm{1}+\mathrm{x}^{\mathrm{2}} \:=\:\frac{\mathrm{cos}\:^{\mathrm{2}} \mathrm{q}+\mathrm{1}+\mathrm{2sin}\:\mathrm{q}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{q}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{q}} \\ $$$$\:\Leftrightarrow\:\frac{\mathrm{2}+\mathrm{2sin}\:\mathrm{q}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{q}}\:\mathrm{then}\:\mathrm{x}^{\mathrm{2}} +\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{sin}\:\mathrm{q}\:= \\ $$$$\frac{\mathrm{1}+\mathrm{2sin}\:\mathrm{q}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{q}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{q}}\:+\:\left(\frac{\mathrm{2}+\mathrm{2sin}\:\mathrm{q}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{q}}\right).\mathrm{sin}\:\mathrm{q}= \\ $$$$\:\frac{\mathrm{1}+\mathrm{4sin}\:\mathrm{q}+\mathrm{3sin}\:^{\mathrm{2}} \mathrm{q}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{q}}\:=\:\frac{\mathrm{4sin}\:^{\mathrm{2}} \mathrm{q}+\mathrm{4sin}\:\mathrm{q}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{q}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{q}} \\ $$$$\:=\:\mathrm{1}+\frac{\mathrm{4sin}\:\mathrm{q}\left(\mathrm{sin}\:\mathrm{q}+\mathrm{1}\right)}{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{q}}\: \\ $$$$\:=\:\mathrm{1}+\:\frac{\mathrm{4sin}\:\mathrm{q}}{\mathrm{1}−\mathrm{sin}\:\mathrm{q}}\:=\:\mathrm{1}+\:\frac{\mathrm{4}}{\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{q}}\:−\mathrm{1}} \\ $$$$ \\ $$
