If-x-is-a-real-number-and-y-is-equal-to-x-2-1-x-2-x-1-show-that-y-4-3-2-3-

Question Number 152063 by Tawa11 last updated on 25/Aug/21

If x is a real number and y is equal to \frac{x^{2} + 1}{x^{2} + x + 1},

show that ∣ y - \frac{4}{3} ∣ ⩽ \frac{2}{3}

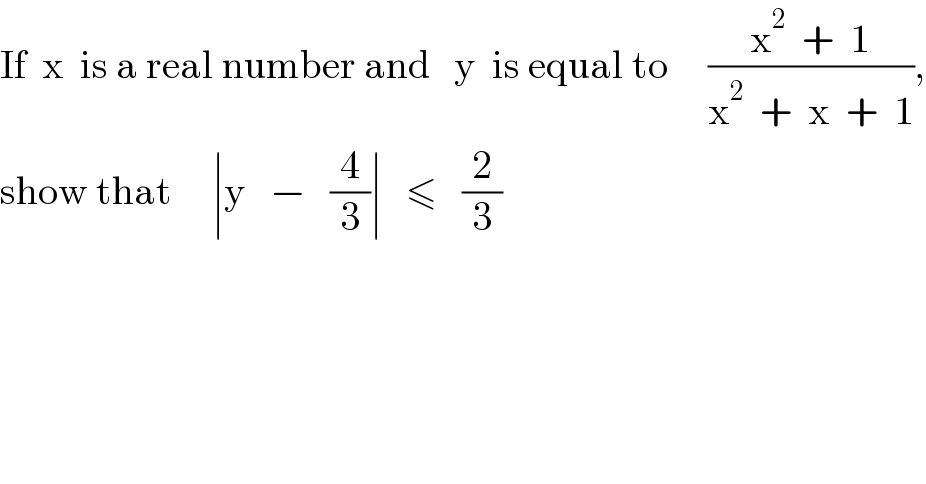
Answered by mr W last updated on 25/Aug/21

y = \frac{x^{2} + 1}{x^{2} + x + 1}

y = 1 - \frac{x}{x^{2} + x + 1}

y = 1 - \frac{1}{x + \frac{1}{x} + 1}

x + \frac{1}{x} ⩾ 2 f o r x > 0

x + \frac{1}{x} ⩽ - 2 f o r x < 0

y_{m a x} = 1 - \frac{1}{- 2 + 1} = 2

y_{m i n} = 1 - \frac{1}{2 + 1} = \frac{2}{3}

\Rightarrow \frac{2}{3} ⩽ y ⩽ 2

\Rightarrow - \frac{2}{3} ⩽ y - \frac{4}{3} ⩽ \frac{2}{3}

\Rightarrow∣ y - \frac{4}{3} ∣⩽ \frac{2}{3}

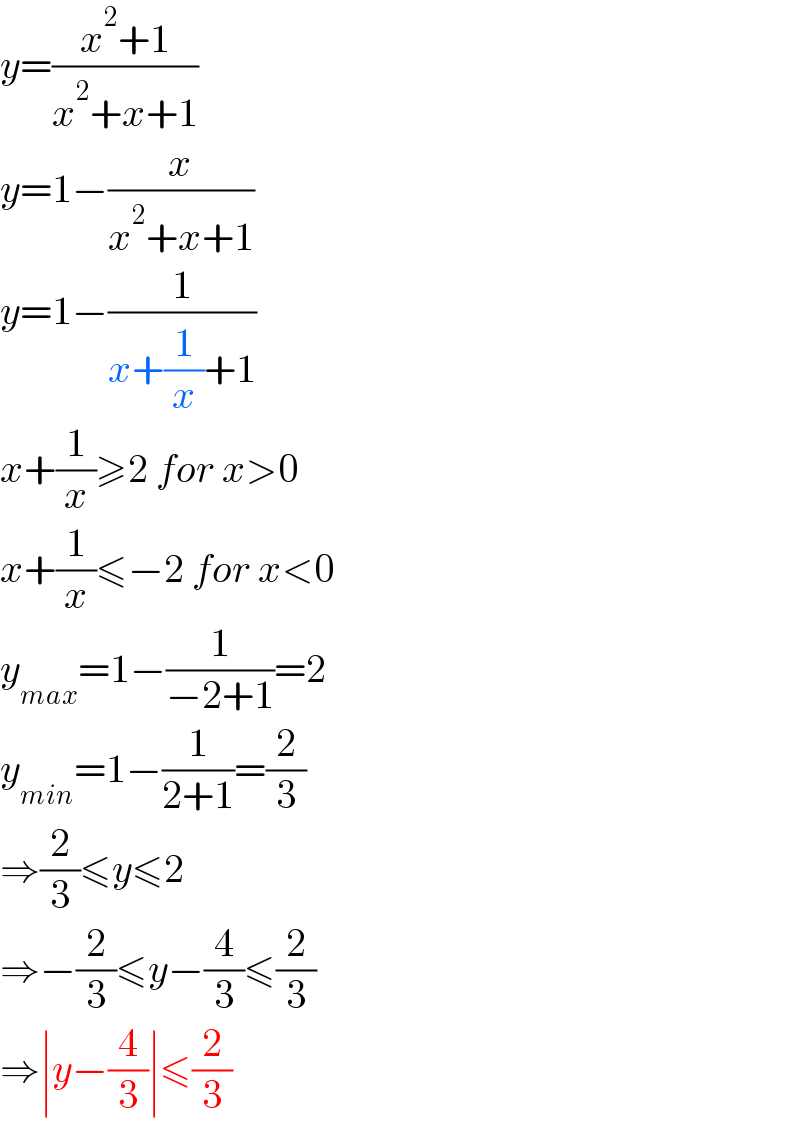
Commented by Tawa11 last updated on 25/Aug/21

Thanks sir . God bless you .

Commented by otchereabdullai@gmail.com last updated on 25/Aug/21

wow!

Answered by john_santu last updated on 25/Aug/21

y = \frac{x^{2} + 1}{x^{2} + x + 1} \Rightarrow {yx}^{2} + yx + y = x^{2} + 1

\Rightarrow (y - 1) x^{2} + yx + y - 1 = 0

Δ ⩾ 0 \Rightarrow y^{2} - 4 {(y - 1)}^{2} ⩾ 0

\Rightarrow y^{2} - {(2 y - 2)}^{2} ⩾ 0

\Rightarrow (3 y - 2) (- y + 2) ⩾ 0

\Rightarrow (3 y - 2) (y - 2) ⩽ 0

\Rightarrow \frac{2}{3} ⩽ y ⩽ 2; \frac{2}{3} - \frac{4}{3} ⩽ y - \frac{4}{3} ⩽ 2 - \frac{4}{3}

\Rightarrow - \frac{2}{3} ⩽ y - \frac{4}{3} ⩽ \frac{2}{3}

\Rightarrow ∣ y - \frac{4}{3} ∣⩽ \frac{2}{3} .

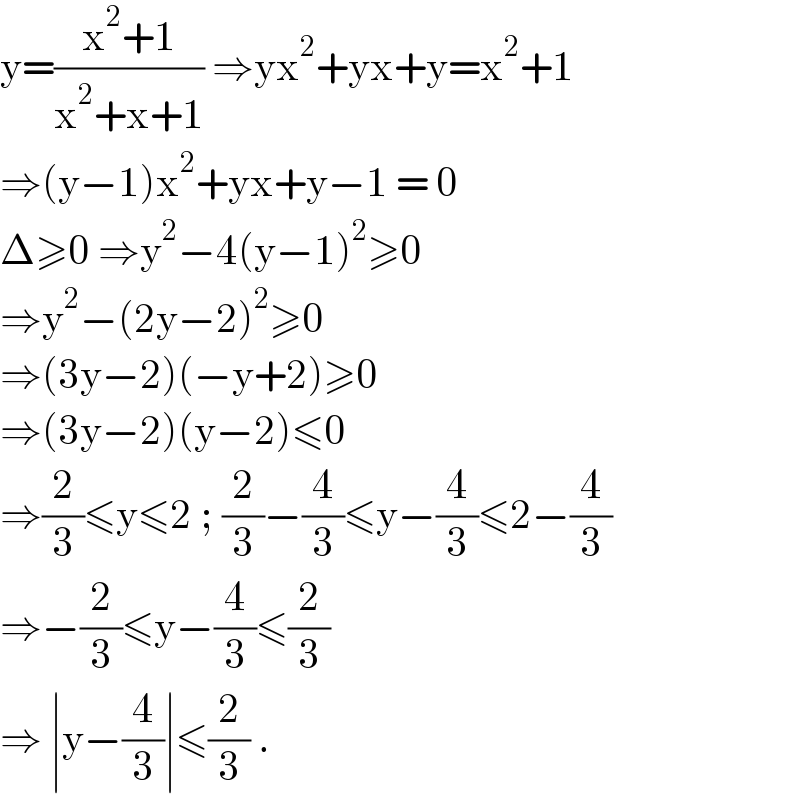
Commented by Tawa11 last updated on 25/Aug/21

Thanks sir . God bless you .

Facebook Tweet Pin