Question Number 152203 by peter frank last updated on 26/Aug/21
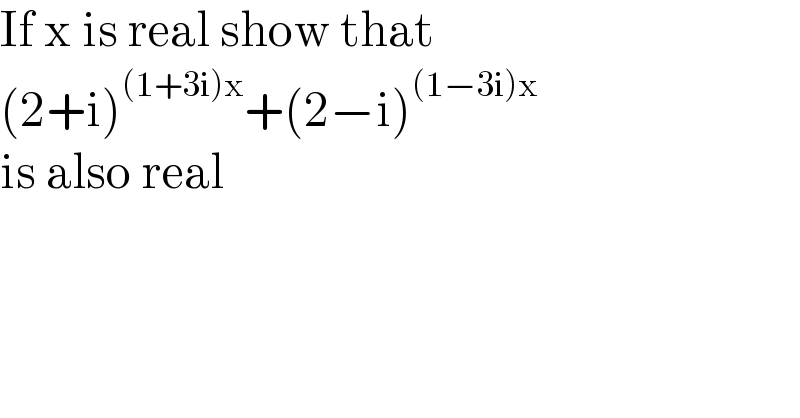
$$\mathrm{If}\:\mathrm{x}\:\mathrm{is}\:\mathrm{real}\:\mathrm{show}\:\mathrm{that} \\ $$$$\left(\mathrm{2}+\mathrm{i}\right)^{\left(\mathrm{1}+\mathrm{3i}\right)\mathrm{x}} +\left(\mathrm{2}−\mathrm{i}\right)^{\left(\mathrm{1}−\mathrm{3i}\right)\mathrm{x}} \\ $$$$\mathrm{is}\:\mathrm{also}\:\mathrm{real} \\ $$
Commented by MJS_new last updated on 26/Aug/21
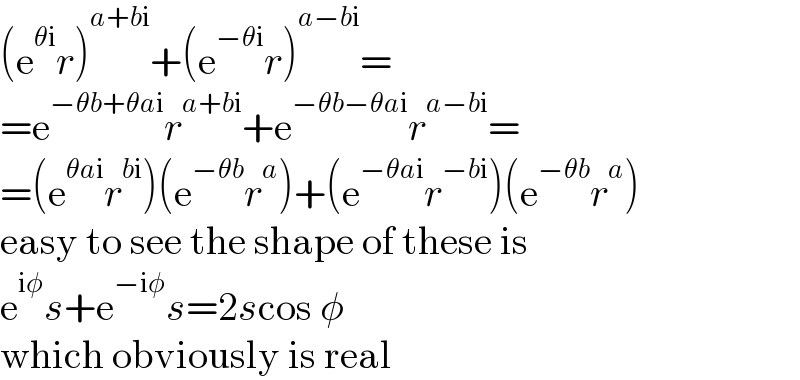
$$\left(\mathrm{e}^{\theta\mathrm{i}} {r}\right)^{{a}+{b}\mathrm{i}} +\left(\mathrm{e}^{−\theta\mathrm{i}} {r}\right)^{{a}−{b}\mathrm{i}} = \\ $$$$=\mathrm{e}^{−\theta{b}+\theta{a}\mathrm{i}} {r}^{{a}+{b}\mathrm{i}} +\mathrm{e}^{−\theta{b}−\theta{a}\mathrm{i}} {r}^{{a}−{b}\mathrm{i}} = \\ $$$$=\left(\mathrm{e}^{\theta{a}\mathrm{i}} {r}^{{b}\mathrm{i}} \right)\left(\mathrm{e}^{−\theta{b}} {r}^{{a}} \right)+\left(\mathrm{e}^{−\theta{a}\mathrm{i}} {r}^{−{b}\mathrm{i}} \right)\left(\mathrm{e}^{−\theta{b}} {r}^{{a}} \right) \\ $$$$\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:\mathrm{the}\:\mathrm{shape}\:\mathrm{of}\:\mathrm{these}\:\mathrm{is} \\ $$$$\mathrm{e}^{\mathrm{i}\phi} {s}+\mathrm{e}^{−\mathrm{i}\phi} {s}=\mathrm{2}{s}\mathrm{cos}\:\phi \\ $$$$\mathrm{which}\:\mathrm{obviously}\:\mathrm{is}\:\mathrm{real} \\ $$
