Question Number 151179 by mathdanisur last updated on 18/Aug/21
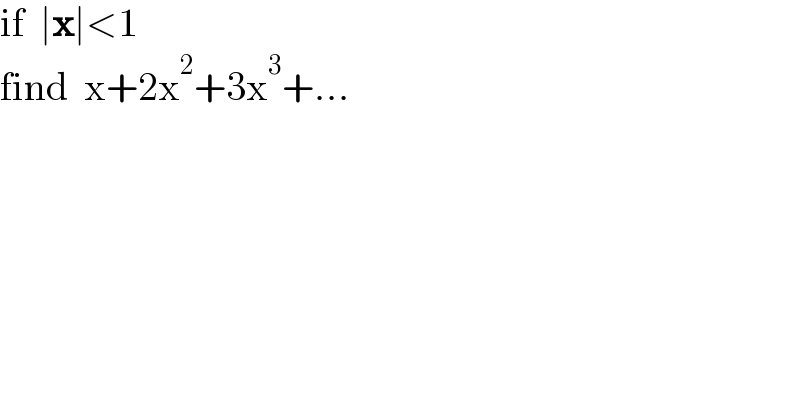
$$\mathrm{if}\:\:\mid\boldsymbol{\mathrm{x}}\mid<\mathrm{1} \\ $$$$\mathrm{find}\:\:\mathrm{x}+\mathrm{2x}^{\mathrm{2}} +\mathrm{3x}^{\mathrm{3}} +… \\ $$
Answered by Olaf_Thorendsen last updated on 18/Aug/21
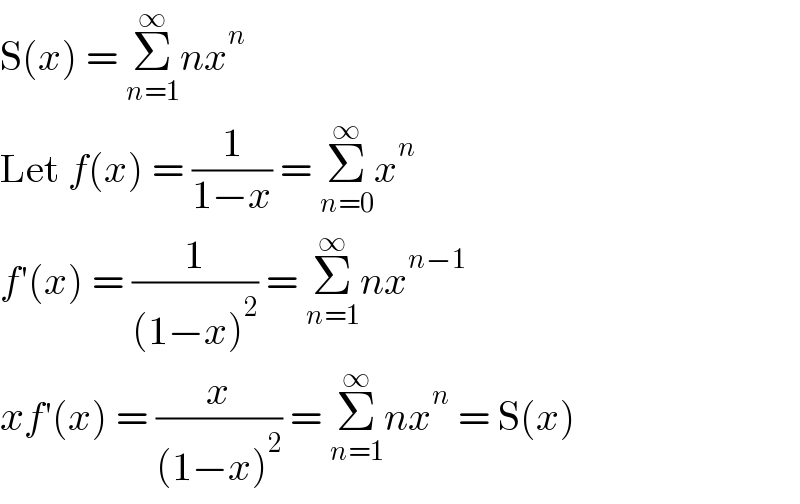
$$\mathrm{S}\left({x}\right)\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{nx}^{{n}} \\ $$$$\mathrm{Let}\:{f}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}−{x}}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{n}} \\ $$$${f}'\left({x}\right)\:=\:\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{nx}^{{n}−\mathrm{1}} \\ $$$${xf}'\left({x}\right)\:=\:\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{nx}^{{n}} \:=\:\mathrm{S}\left({x}\right) \\ $$
Commented by mathdanisur last updated on 18/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$
Answered by qaz last updated on 19/Aug/21

$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{nx}^{\mathrm{n}} \\ $$$$=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{x}^{\mathrm{n}} \\ $$$$=\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{x}^{\mathrm{n}+\mathrm{k}} \\ $$$$=\left(\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{x}^{\mathrm{k}} \right)\left(\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{x}^{\mathrm{n}} \right) \\ $$$$=\frac{\mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} } \\ $$
Commented by mathdanisur last updated on 19/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$
