Question Number 35246 by JOHNMASANJA last updated on 17/May/18
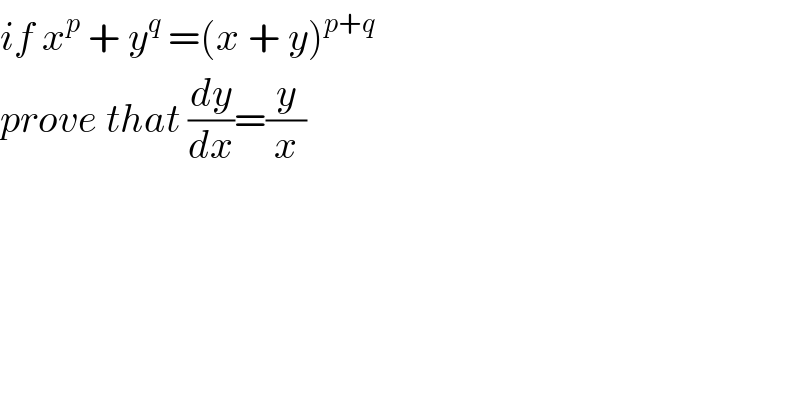
$${if}\:{x}^{{p}} \:+\:{y}^{{q}} \:=\left({x}\:+\:{y}\right)^{{p}+{q}} \: \\ $$$${prove}\:{that}\:\frac{{dy}}{{dx}}=\frac{{y}}{{x}} \\ $$
Commented by math1967 last updated on 17/May/18

$${plz}.\:{check}\:{question} \\ $$$${x}^{{p}} +{y}^{{q}} \:{ORx}^{{p}} .{y}^{{q}} \:????????????????? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 18/May/18

$$\frac{{dy}}{{y}}−\frac{{dx}}{{x}}=\mathrm{0} \\ $$$$\int\frac{{dy}}{{y}}=\int\frac{{dx}}{{x}} \\ $$$${lny}={lnx}+{lnk} \\ $$$${ln}\left(\frac{{y}}{{x}}\right)={lnk} \\ $$$${y}={xk} \\ $$$${now}\:{put} \\ $$$${y}={xk}\:{in}\:{the}\:{given}\:{expression} \\ $$$${LHS}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$${x}^{{p}} +{y}^{{q}} \\ $$$${x}^{{p}} +{x}^{{q}} {k}^{{q}} \\ $$$${RHS} \\ $$$$\left({x}+{y}\right)^{{p}+{q}} \\ $$$$\left({x}+{xk}\right)^{{p}+{a}} \\ $$$${x}^{{p}+{q}} ×\left(\mathrm{1}+{k}\right)^{{p}+{q}} \\ $$$${so}\:{LHS}\:{not}\:{equals}\:{to}\:{RHS}\:{so}\:{question}\:{is}\:{wrong} \\ $$$${i}\:{think}…. \\ $$$$ \\ $$
