Question Number 151475 by mathdanisur last updated on 21/Aug/21
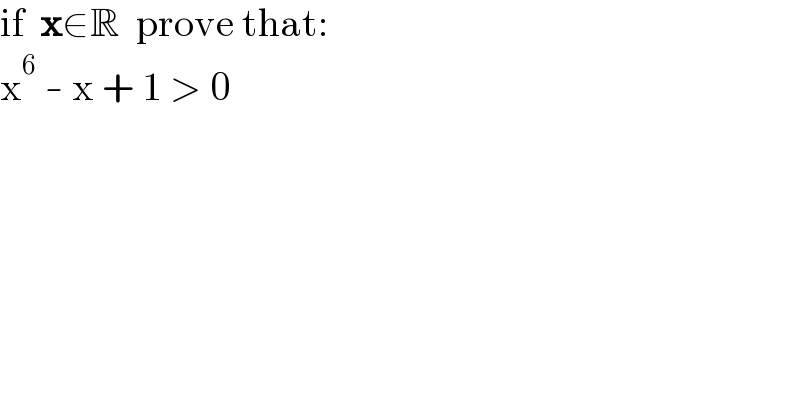
$$\mathrm{if}\:\:\boldsymbol{\mathrm{x}}\in\mathbb{R}\:\:\mathrm{prove}\:\mathrm{that}: \\ $$$$\mathrm{x}^{\mathrm{6}} \:-\:\mathrm{x}\:+\:\mathrm{1}\:>\:\mathrm{0} \\ $$
Answered by dumitrel last updated on 21/Aug/21
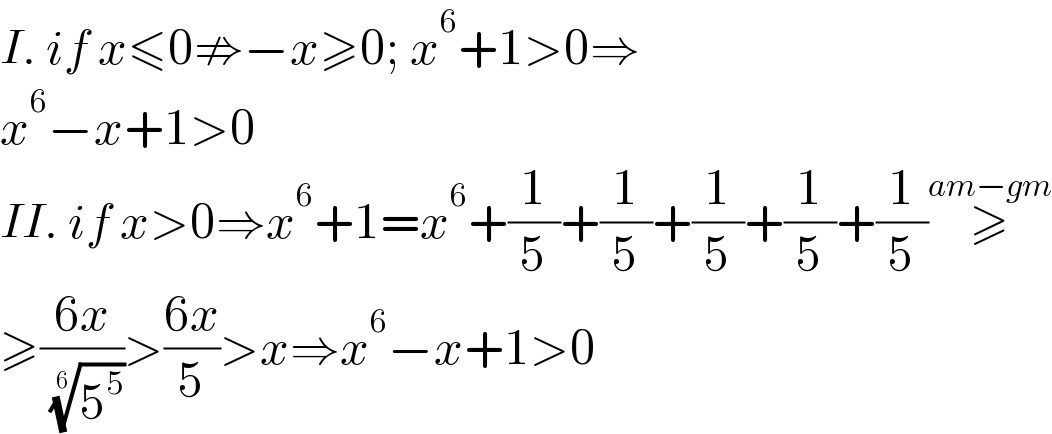
$${I}.\:{if}\:{x}\leqslant\mathrm{0}\nRightarrow−{x}\geqslant\mathrm{0};\:{x}^{\mathrm{6}} +\mathrm{1}>\mathrm{0}\Rightarrow \\ $$$${x}^{\mathrm{6}} −{x}+\mathrm{1}>\mathrm{0} \\ $$$${II}.\:{if}\:{x}>\mathrm{0}\Rightarrow{x}^{\mathrm{6}} +\mathrm{1}={x}^{\mathrm{6}} +\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{5}}\overset{{am}−{gm}} {\geqslant} \\ $$$$\geqslant\frac{\mathrm{6}{x}}{\:\sqrt[{\mathrm{6}}]{\mathrm{5}^{\mathrm{5}} }}>\frac{\mathrm{6}{x}}{\mathrm{5}}>{x}\Rightarrow{x}^{\mathrm{6}} −{x}+\mathrm{1}>\mathrm{0} \\ $$
Commented by mathdanisur last updated on 21/Aug/21
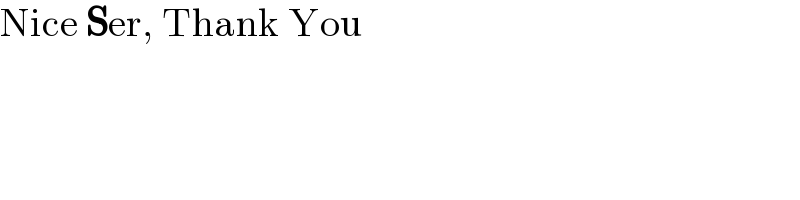
$$\mathrm{Nice}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{Thank}\:\mathrm{You} \\ $$
Answered by MJS_new last updated on 21/Aug/21
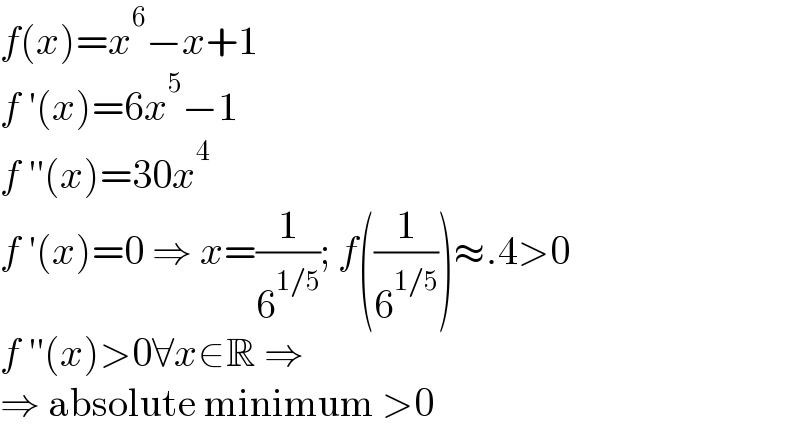
$${f}\left({x}\right)={x}^{\mathrm{6}} −{x}+\mathrm{1} \\ $$$${f}\:'\left({x}\right)=\mathrm{6}{x}^{\mathrm{5}} −\mathrm{1} \\ $$$${f}\:''\left({x}\right)=\mathrm{30}{x}^{\mathrm{4}} \\ $$$${f}\:'\left({x}\right)=\mathrm{0}\:\Rightarrow\:{x}=\frac{\mathrm{1}}{\mathrm{6}^{\mathrm{1}/\mathrm{5}} };\:{f}\left(\frac{\mathrm{1}}{\mathrm{6}^{\mathrm{1}/\mathrm{5}} }\right)\approx.\mathrm{4}>\mathrm{0} \\ $$$${f}\:''\left({x}\right)>\mathrm{0}\forall{x}\in\mathbb{R}\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{absolute}\:\mathrm{minimum}\:>\mathrm{0} \\ $$
