Question Number 162371 by cortano last updated on 29/Dec/21
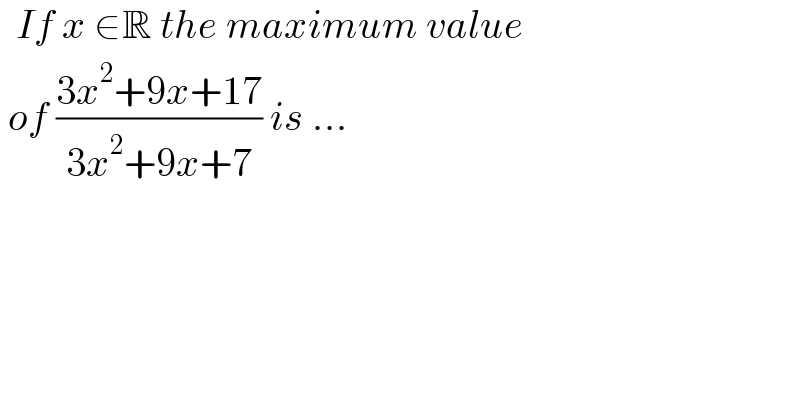
$$\:\:{If}\:{x}\:\in\mathbb{R}\:{the}\:{maximum}\:{value}\: \\ $$$$\:{of}\:\frac{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{9}{x}+\mathrm{17}}{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{9}{x}+\mathrm{7}}\:{is}\:… \\ $$
Answered by mindispower last updated on 29/Dec/21
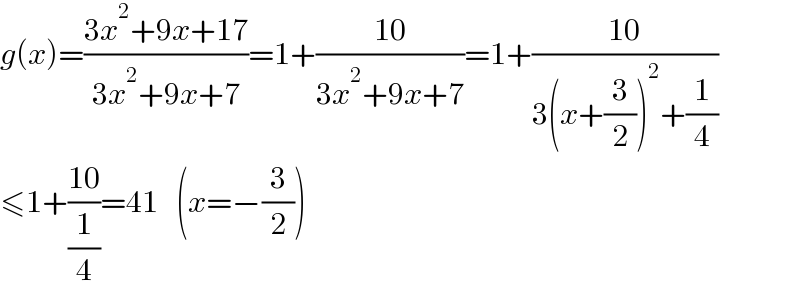
$${g}\left({x}\right)=\frac{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{9}{x}+\mathrm{17}}{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{9}{x}+\mathrm{7}}=\mathrm{1}+\frac{\mathrm{10}}{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{9}{x}+\mathrm{7}}=\mathrm{1}+\frac{\mathrm{10}}{\mathrm{3}\left({x}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$\leqslant\mathrm{1}+\frac{\mathrm{10}}{\frac{\mathrm{1}}{\mathrm{4}}}=\mathrm{41}\:\:\:\left({x}=−\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$
Answered by bobhans last updated on 29/Dec/21
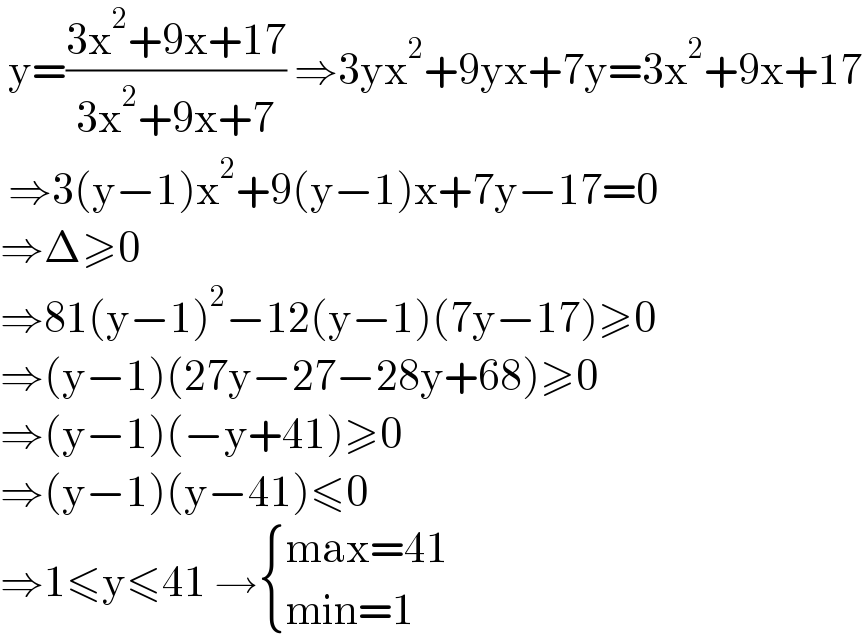
$$\:\mathrm{y}=\frac{\mathrm{3x}^{\mathrm{2}} +\mathrm{9x}+\mathrm{17}}{\mathrm{3x}^{\mathrm{2}} +\mathrm{9x}+\mathrm{7}}\:\Rightarrow\mathrm{3yx}^{\mathrm{2}} +\mathrm{9yx}+\mathrm{7y}=\mathrm{3x}^{\mathrm{2}} +\mathrm{9x}+\mathrm{17} \\ $$$$\:\Rightarrow\mathrm{3}\left(\mathrm{y}−\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} +\mathrm{9}\left(\mathrm{y}−\mathrm{1}\right)\mathrm{x}+\mathrm{7y}−\mathrm{17}=\mathrm{0} \\ $$$$\Rightarrow\Delta\geqslant\mathrm{0}\: \\ $$$$\Rightarrow\mathrm{81}\left(\mathrm{y}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{12}\left(\mathrm{y}−\mathrm{1}\right)\left(\mathrm{7y}−\mathrm{17}\right)\geqslant\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{y}−\mathrm{1}\right)\left(\mathrm{27y}−\mathrm{27}−\mathrm{28y}+\mathrm{68}\right)\geqslant\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{y}−\mathrm{1}\right)\left(−\mathrm{y}+\mathrm{41}\right)\geqslant\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{y}−\mathrm{1}\right)\left(\mathrm{y}−\mathrm{41}\right)\leqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}\leqslant\mathrm{y}\leqslant\mathrm{41}\:\rightarrow\begin{cases}{\mathrm{max}=\mathrm{41}}\\{\mathrm{min}=\mathrm{1}}\end{cases} \\ $$
