Question Number 160550 by HongKing last updated on 01/Dec/21
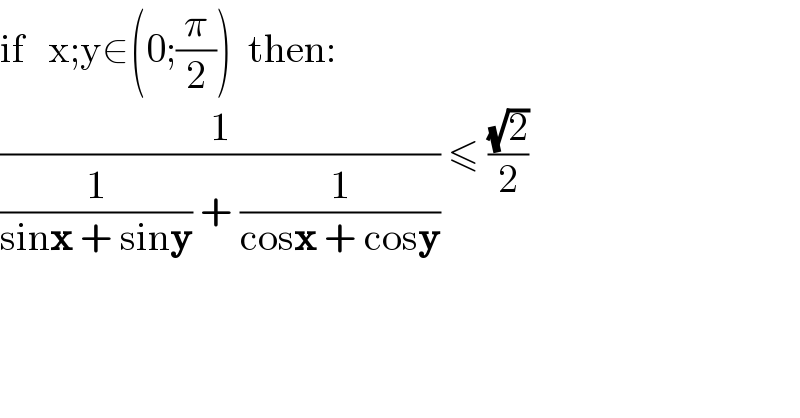
$$\mathrm{if}\:\:\:\mathrm{x};\mathrm{y}\in\left(\mathrm{0};\frac{\pi}{\mathrm{2}}\right)\:\:\mathrm{then}: \\ $$$$\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{sin}\boldsymbol{\mathrm{x}}\:+\:\mathrm{sin}\boldsymbol{\mathrm{y}}}\:+\:\frac{\mathrm{1}}{\mathrm{cos}\boldsymbol{\mathrm{x}}\:+\:\mathrm{cos}\boldsymbol{\mathrm{y}}}}\:\leqslant\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$
Answered by mr W last updated on 02/Dec/21

$${LHS} \\ $$$$\leqslant\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{sin}\:{x}\:\mathrm{sin}\:{y}}}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{cos}\:{x}\:\mathrm{cos}\:{y}}}} \\ $$$$\leqslant\frac{\mathrm{2}}{\mathrm{2}\sqrt{\sqrt{\frac{\mathrm{1}}{\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}\:\mathrm{sin}\:{y}\:\mathrm{cos}\:{y}}}}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\sqrt{\frac{\mathrm{4}}{\mathrm{sin}\:\mathrm{2}{x}\:\mathrm{sin}\:\mathrm{2}{y}}}}} \\ $$$$=\frac{\sqrt{\sqrt{\mathrm{sin}\:\mathrm{2}{x}\:\mathrm{sin}\:\mathrm{2}{y}}}}{\:\sqrt{\mathrm{2}}} \\ $$$$\leqslant\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$
Commented by HongKing last updated on 02/Dec/21

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{my}\:\mathrm{dear}\:\boldsymbol{\mathrm{Sir}}\:\mathrm{cool} \\ $$
