Question Number 150006 by mathdanisur last updated on 08/Aug/21

Answered by dumitrel last updated on 08/Aug/21
![xy=k⇒x+(k/x)=(1/2)⇒2x^2 −x+2k=0⇒△≥0⇒ 1−16k≥0⇒k∈(−∞;(1/(16))]⇒k∉((1/(16));∞)](https://www.tinkutara.com/question/Q150015.png)
Commented by mathdanisur last updated on 08/Aug/21

Commented by mathdanisur last updated on 08/Aug/21
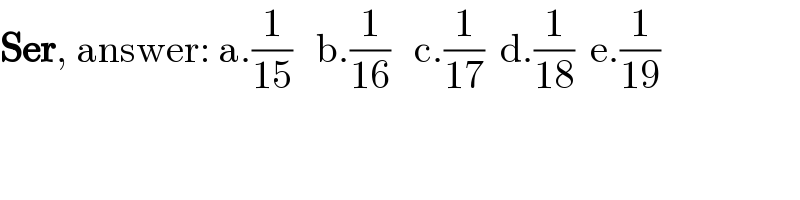
Commented by dumitrel last updated on 08/Aug/21

Commented by mathdanisur last updated on 08/Aug/21

Commented by dumitrel last updated on 08/Aug/21

