Question Number 112461 by dw last updated on 08/Sep/20
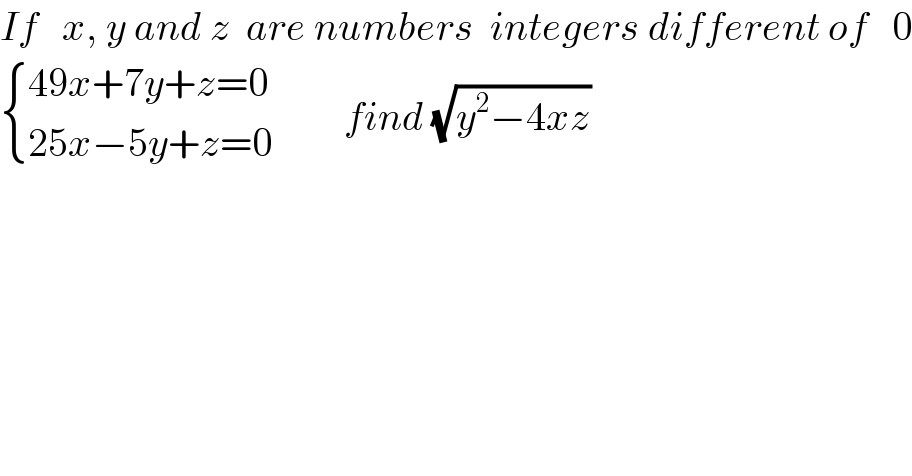
$${If}\:\:\:{x},\:{y}\:{and}\:{z}\:\:{are}\:{numbers}\:\:{integers}\:{different}\:{of}\:\:\:\mathrm{0} \\ $$$$\begin{cases}{\mathrm{49}{x}+\mathrm{7}{y}+{z}=\mathrm{0}}\\{\mathrm{25}{x}−\mathrm{5}{y}+{z}=\mathrm{0}}\end{cases}\:\:\:\:\:\:\:\:\:{find}\:\sqrt{{y}^{\mathrm{2}} −\mathrm{4}{xz}} \\ $$
Answered by floor(10²Eta[1]) last updated on 08/Sep/20
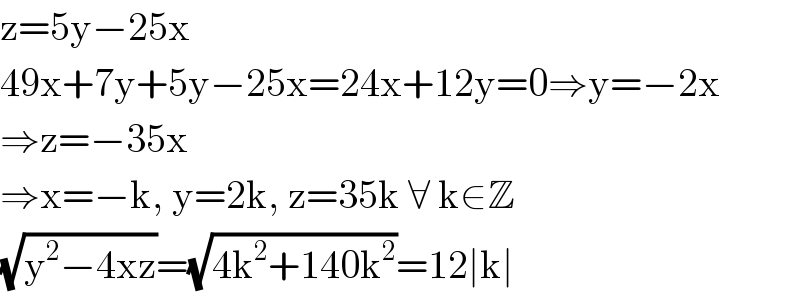
$$\mathrm{z}=\mathrm{5y}−\mathrm{25x} \\ $$$$\mathrm{49x}+\mathrm{7y}+\mathrm{5y}−\mathrm{25x}=\mathrm{24x}+\mathrm{12y}=\mathrm{0}\Rightarrow\mathrm{y}=−\mathrm{2x} \\ $$$$\Rightarrow\mathrm{z}=−\mathrm{35x} \\ $$$$\Rightarrow\mathrm{x}=−\mathrm{k},\:\mathrm{y}=\mathrm{2k},\:\mathrm{z}=\mathrm{35k}\:\forall\:\mathrm{k}\in\mathbb{Z} \\ $$$$\sqrt{\mathrm{y}^{\mathrm{2}} −\mathrm{4xz}}=\sqrt{\mathrm{4k}^{\mathrm{2}} +\mathrm{140k}^{\mathrm{2}} }=\mathrm{12}\mid\mathrm{k}\mid \\ $$
Commented by dw last updated on 08/Sep/20

$${Thank}\:{you}\:{Sir} \\ $$
