Question Number 144917 by mathdanisur last updated on 30/Jun/21
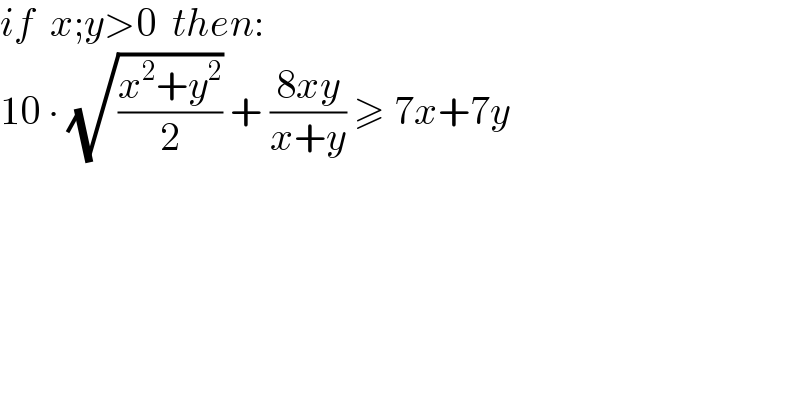
$${if}\:\:{x};{y}>\mathrm{0}\:\:{then}: \\ $$$$\mathrm{10}\:\centerdot\:\sqrt{\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}}}\:+\:\frac{\mathrm{8}{xy}}{{x}+{y}}\:\geqslant\:\mathrm{7}{x}+\mathrm{7}{y} \\ $$
Answered by justtry last updated on 30/Jun/21
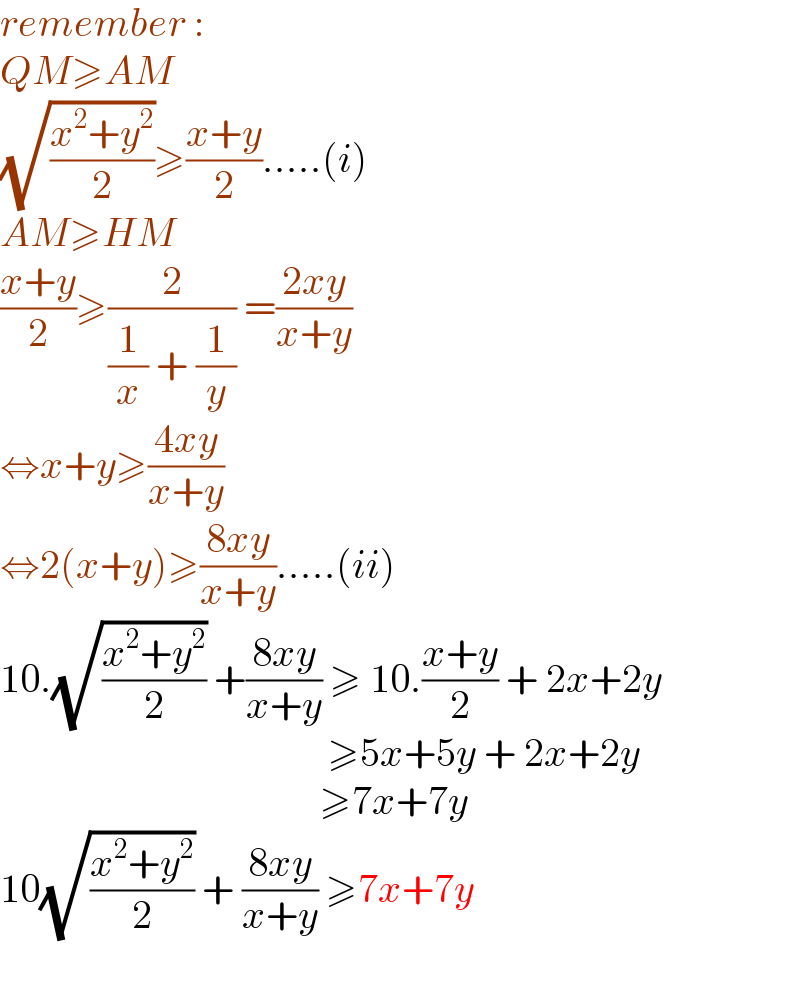
$${remember}\:: \\ $$$${QM}\geqslant{AM} \\ $$$$\sqrt{\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}}}\geqslant\frac{{x}+{y}}{\mathrm{2}}…..\left({i}\right) \\ $$$${AM}\geqslant{HM} \\ $$$$\frac{{x}+{y}}{\mathrm{2}}\geqslant\frac{\mathrm{2}}{\frac{\mathrm{1}}{{x}}\:+\:\frac{\mathrm{1}}{{y}}}\:=\frac{\mathrm{2}{xy}}{{x}+{y}}\: \\ $$$$\Leftrightarrow{x}+{y}\geqslant\frac{\mathrm{4}{xy}}{{x}+{y}} \\ $$$$\Leftrightarrow\mathrm{2}\left({x}+{y}\right)\geqslant\frac{\mathrm{8}{xy}}{{x}+{y}}…..\left({ii}\right) \\ $$$$\mathrm{10}.\sqrt{\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}}}\:+\frac{\mathrm{8}{xy}}{{x}+{y}}\:\geqslant\:\mathrm{10}.\frac{{x}+{y}}{\mathrm{2}}\:+\:\mathrm{2}{x}+\mathrm{2}{y} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\geqslant\mathrm{5}{x}+\mathrm{5}{y}\:+\:\mathrm{2}{x}+\mathrm{2}{y} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\geqslant\mathrm{7}{x}+\mathrm{7}{y} \\ $$$$\mathrm{10}\sqrt{\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}}}\:+\:\frac{\mathrm{8}{xy}}{{x}+{y}}\:\geqslant\mathrm{7}{x}+\mathrm{7}{y} \\ $$$$ \\ $$
Commented by mathdanisur last updated on 30/Jun/21
$${cool}\:{Sir},\:{thank}\:{you} \\ $$
