Question Number 157871 by HongKing last updated on 29/Oct/21
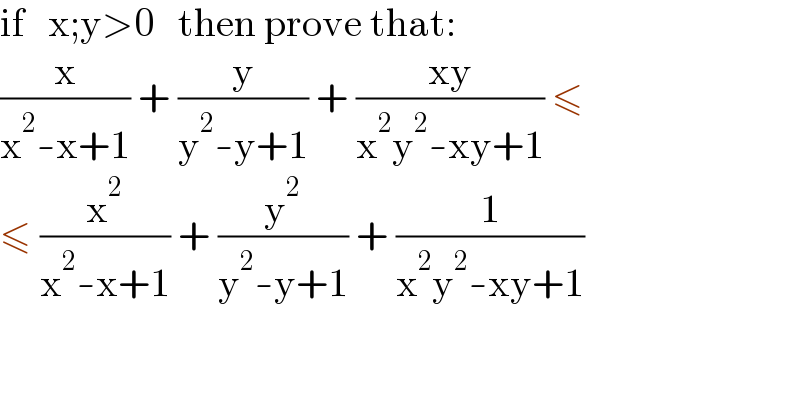
$$\mathrm{if}\:\:\:\mathrm{x};\mathrm{y}>\mathrm{0}\:\:\:\mathrm{then}\:\mathrm{prove}\:\mathrm{that}: \\ $$$$\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} -\mathrm{x}+\mathrm{1}}\:+\:\frac{\mathrm{y}}{\mathrm{y}^{\mathrm{2}} -\mathrm{y}+\mathrm{1}}\:+\:\frac{\mathrm{xy}}{\mathrm{x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} -\mathrm{xy}+\mathrm{1}}\:\leqslant \\ $$$$\leqslant\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} -\mathrm{x}+\mathrm{1}}\:+\:\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{y}^{\mathrm{2}} -\mathrm{y}+\mathrm{1}}\:+\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} -\mathrm{xy}+\mathrm{1}} \\ $$
