Question Number 20851 by j.masanja06@gmail.com last updated on 04/Sep/17
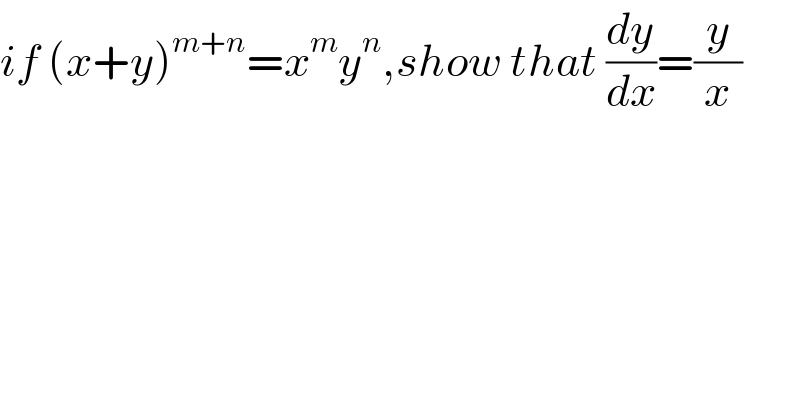
$${if}\:\left({x}+{y}\right)^{{m}+{n}} ={x}^{{m}} {y}^{{n}} ,{show}\:{that}\:\frac{{dy}}{{dx}}=\frac{{y}}{{x}} \\ $$
Answered by ajfour last updated on 04/Sep/17
![taking logarithm on both sides: (m+n)ln (x+y)=mln x+nln y (((m+n)/(x+y)))(1+(dy/dx))=(m/x)+(n/y)((dy/dx)) ⇒ (dy/dx)(((m+n)/(x+y))−(n/y))=(m/x)−((m+n)/(x+y)) or (dy/dx)[((my−nx)/(y(x+y)))]=((my−nx)/(x(x+y))) if my≠nx and x≠y then (dy/dx)=(y/x) .](https://www.tinkutara.com/question/Q20852.png)
$${taking}\:{logarithm}\:{on}\:{both}\:{sides}: \\ $$$$\left({m}+{n}\right)\mathrm{ln}\:\left({x}+{y}\right)={m}\mathrm{ln}\:{x}+{n}\mathrm{ln}\:{y} \\ $$$$\left(\frac{{m}+{n}}{{x}+{y}}\right)\left(\mathrm{1}+\frac{{dy}}{{dx}}\right)=\frac{{m}}{{x}}+\frac{{n}}{{y}}\left(\frac{{dy}}{{dx}}\right) \\ $$$$\Rightarrow\:\:\frac{{dy}}{{dx}}\left(\frac{{m}+{n}}{{x}+{y}}−\frac{{n}}{{y}}\right)=\frac{{m}}{{x}}−\frac{{m}+{n}}{{x}+{y}} \\ $$$${or}\:\:\:\frac{{dy}}{{dx}}\left[\frac{{my}−{nx}}{{y}\left({x}+{y}\right)}\right]=\frac{{my}−{nx}}{{x}\left({x}+{y}\right)} \\ $$$${if}\:{my}\neq{nx}\:\:{and}\:\:{x}\neq{y}\:\:\:{then} \\ $$$$\:\:\:\:\:\:\:\:\frac{{dy}}{{dx}}=\frac{{y}}{{x}}\:. \\ $$
Answered by Bruce Lee last updated on 05/Sep/17

$$\boldsymbol{{take}}\:\boldsymbol{{both}}\:\boldsymbol{{side}}\:\boldsymbol{{by}}\:\boldsymbol{{ln}} \\ $$$$\:\:\Rightarrow\left(\boldsymbol{{m}}+\boldsymbol{{n}}\right)\boldsymbol{{ln}}\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)=\boldsymbol{{mlnx}}+\boldsymbol{{nlny}} \\ $$$$\boldsymbol{{derivative}}\:\boldsymbol{{both}}\:\boldsymbol{{side}} \\ $$$$\boldsymbol{{we}}\:\boldsymbol{{get}}: \\ $$$$\:\:\left(\boldsymbol{{m}}+\boldsymbol{{n}}\right)^{'} \boldsymbol{{ln}}\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)+\left(\boldsymbol{{m}}+\boldsymbol{{n}}\right)\left(\boldsymbol{{ln}}\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)\right)'=\frac{\boldsymbol{{m}}}{\boldsymbol{{x}}}+\frac{\boldsymbol{{ny}}^{'} }{\boldsymbol{{y}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\left(\boldsymbol{{m}}+\boldsymbol{{n}}\right)\frac{\boldsymbol{{y}}^{'} }{\boldsymbol{{x}}+\boldsymbol{{y}}}=\frac{\boldsymbol{{m}}}{\boldsymbol{{x}}}+\frac{\boldsymbol{{ny}}^{'} }{\boldsymbol{{y}}} \\ $$$$\left(\boldsymbol{{m}}+\boldsymbol{{n}}\right)\frac{\boldsymbol{{y}}'}{\boldsymbol{{x}}+\boldsymbol{{y}}}−\frac{\boldsymbol{{ny}}'}{\boldsymbol{{y}}}=\frac{\boldsymbol{{m}}}{\boldsymbol{{x}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\boldsymbol{{y}}'\left(\frac{\boldsymbol{{m}}+\boldsymbol{{n}}}{\boldsymbol{{x}}+\boldsymbol{{y}}}−\frac{\boldsymbol{{n}}}{\boldsymbol{{y}}}\right)=\frac{\boldsymbol{{m}}}{\boldsymbol{{x}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\boldsymbol{{y}}'\left(\frac{\boldsymbol{{my}}+\boldsymbol{{ny}}−\boldsymbol{{nx}}−\boldsymbol{{ny}}}{\boldsymbol{{y}}\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)}\right)=\frac{\boldsymbol{{m}}}{\boldsymbol{{x}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{y}}'\centerdot\frac{\boldsymbol{{my}}−\boldsymbol{{nx}}}{\boldsymbol{{y}}\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)}=\frac{\boldsymbol{{m}}}{\boldsymbol{{n}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{y}}'=\frac{\boldsymbol{{m}}}{\boldsymbol{{n}}}\centerdot\frac{\boldsymbol{{y}}\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)}{\boldsymbol{{my}}−\boldsymbol{{nx}}} \\ $$
Commented by Bruce Lee last updated on 05/Sep/17

$$\boldsymbol{\mathrm{thanks}}\:\boldsymbol{\mathrm{you}} \\ $$
Commented by $@ty@m last updated on 05/Sep/17
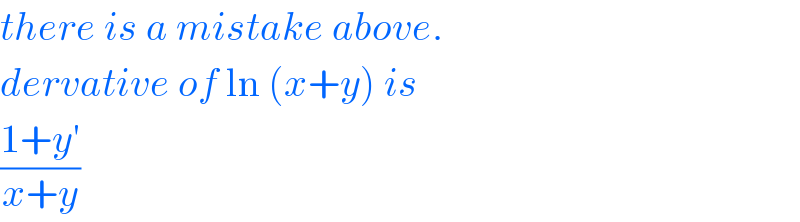
$${there}\:{is}\:{a}\:{mistake}\:{above}. \\ $$$${dervative}\:{of}\:\mathrm{ln}\:\left({x}+{y}\right)\:{is} \\ $$$$\frac{\mathrm{1}+{y}'}{{x}+{y}} \\ $$
