Question Number 116601 by ZiYangLee last updated on 05/Oct/20
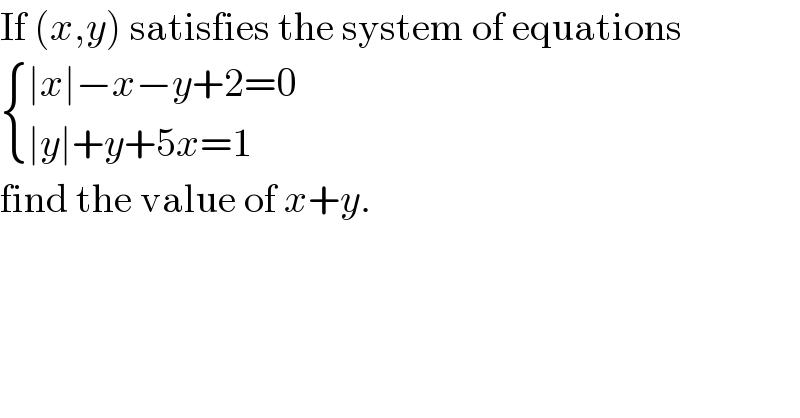
$$\mathrm{If}\:\left({x},{y}\right)\:\mathrm{satisfies}\:\mathrm{the}\:\mathrm{system}\:\mathrm{of}\:\mathrm{equations} \\ $$$$\begin{cases}{\mid{x}\mid−{x}−{y}+\mathrm{2}=\mathrm{0}}\\{\mid{y}\mid+{y}+\mathrm{5}{x}=\mathrm{1}}\end{cases}\: \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{x}+{y}.\: \\ $$
Answered by mr W last updated on 05/Oct/20
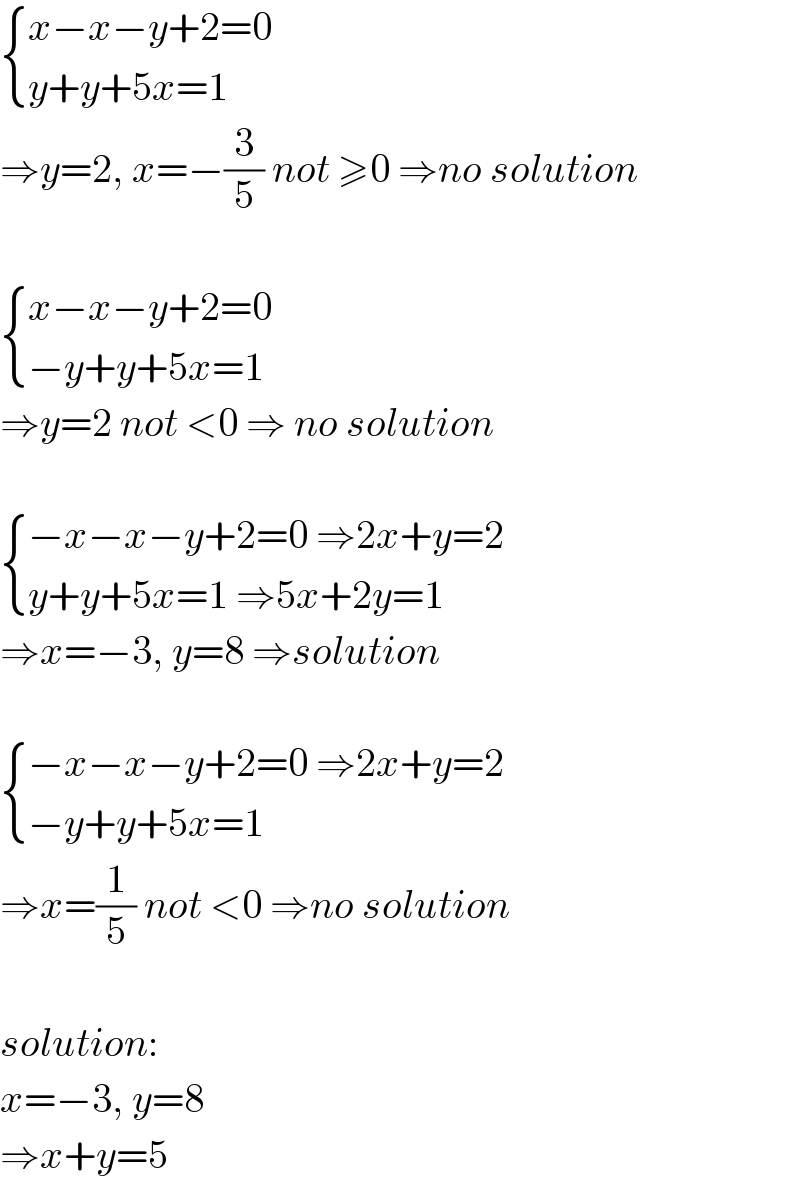
$$\begin{cases}{{x}−{x}−{y}+\mathrm{2}=\mathrm{0}}\\{{y}+{y}+\mathrm{5}{x}=\mathrm{1}}\end{cases}\: \\ $$$$\Rightarrow{y}=\mathrm{2},\:{x}=−\frac{\mathrm{3}}{\mathrm{5}}\:{not}\:\geqslant\mathrm{0}\:\Rightarrow{no}\:{solution} \\ $$$$ \\ $$$$\begin{cases}{{x}−{x}−{y}+\mathrm{2}=\mathrm{0}}\\{−{y}+{y}+\mathrm{5}{x}=\mathrm{1}}\end{cases}\: \\ $$$$\Rightarrow{y}=\mathrm{2}\:{not}\:<\mathrm{0}\:\Rightarrow\:{no}\:{solution} \\ $$$$ \\ $$$$\begin{cases}{−{x}−{x}−{y}+\mathrm{2}=\mathrm{0}\:\Rightarrow\mathrm{2}{x}+{y}=\mathrm{2}}\\{{y}+{y}+\mathrm{5}{x}=\mathrm{1}\:\Rightarrow\mathrm{5}{x}+\mathrm{2}{y}=\mathrm{1}}\end{cases}\: \\ $$$$\Rightarrow{x}=−\mathrm{3},\:{y}=\mathrm{8}\:\Rightarrow{solution} \\ $$$$ \\ $$$$\begin{cases}{−{x}−{x}−{y}+\mathrm{2}=\mathrm{0}\:\Rightarrow\mathrm{2}{x}+{y}=\mathrm{2}}\\{−{y}+{y}+\mathrm{5}{x}=\mathrm{1}}\end{cases}\: \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{5}}\:{not}\:<\mathrm{0}\:\Rightarrow{no}\:{solution} \\ $$$$ \\ $$$${solution}: \\ $$$${x}=−\mathrm{3},\:{y}=\mathrm{8} \\ $$$$\Rightarrow{x}+{y}=\mathrm{5} \\ $$
Commented by ZiYangLee last updated on 05/Oct/20

$$\mathrm{Excellent}\bigstar\bigstar \\ $$
Answered by bemath last updated on 05/Oct/20

$$\begin{cases}{\mid\mathrm{x}\mid=\mathrm{x}+\mathrm{y}−\mathrm{2}}\\{\mid\mathrm{y}\mid=\mathrm{1}−\mathrm{5x}−\mathrm{y}}\end{cases} \\ $$$$\rightarrow\mid\mathrm{x}\mid+\mid\mathrm{y}\mid=−\mathrm{4x}−\mathrm{1}…\left(\mathrm{iii}\right) \\ $$$$\mathrm{case}\left(\mathrm{1}\right)\:\rightarrow\begin{cases}{\mathrm{x}\geqslant\mathrm{0}}\\{\mathrm{y}\geqslant\mathrm{0}}\end{cases}\:\Rightarrow\mathrm{x}+\mathrm{y}=−\mathrm{4x}−\mathrm{1} \\ $$$$\mathrm{y}=−\mathrm{5x}−\mathrm{1}\:\wedge\:\mathrm{2y}=\mathrm{1}−\mathrm{5x} \\ $$$$\mathrm{substitute}\:\Rightarrow\mathrm{2}\left(−\mathrm{5x}−\mathrm{1}\right)=\mathrm{1}−\mathrm{5x} \\ $$$$\Rightarrow−\mathrm{10x}−\mathrm{2}=\mathrm{1}−\mathrm{5x} \\ $$$$\Rightarrow−\mathrm{3}=\mathrm{5x}\:;\:\mathrm{x}=−\frac{\mathrm{3}}{\mathrm{5}}\:\leftarrow\mathrm{rejected} \\ $$$$\mathrm{case}\left(\mathrm{2}\right)\rightarrow\begin{cases}{\mathrm{x}<\mathrm{0}}\\{\mathrm{y}\geqslant\mathrm{0}}\end{cases}\Rightarrow−\mathrm{x}+\mathrm{y}=−\mathrm{4x}−\mathrm{1} \\ $$$$\mathrm{y}=−\mathrm{3x}−\mathrm{1}\:\wedge\:\mathrm{2y}=\mathrm{1}−\mathrm{5x} \\ $$$$\Rightarrow−\mathrm{6x}−\mathrm{2}=\mathrm{1}−\mathrm{5x}\:;\:−\mathrm{x}=\mathrm{3}\:,\:\mathrm{x}=−\mathrm{3}\leftarrow\mathrm{acceptable} \\ $$$$\mathrm{then}\:\mathrm{y}\:=\:\mathrm{9}−\mathrm{1}=\mathrm{8} \\ $$$$\mathrm{therefore}\:\mathrm{x}+\mathrm{y}\:=\:\mathrm{5} \\ $$
Commented by bobhans last updated on 05/Oct/20

$$\mathrm{waw}…..\mathrm{funtastic}.. \\ $$
