Question Number 148746 by mathdanisur last updated on 30/Jul/21
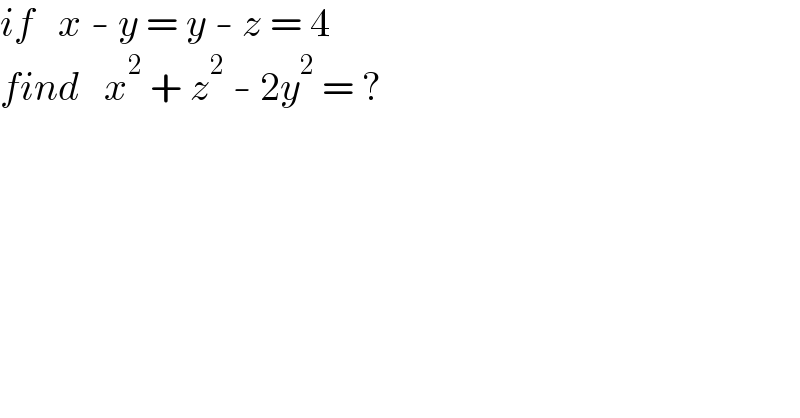
$${if}\:\:\:{x}\:-\:{y}\:=\:{y}\:-\:{z}\:=\:\mathrm{4} \\ $$$${find}\:\:\:{x}^{\mathrm{2}} \:+\:{z}^{\mathrm{2}} \:-\:\mathrm{2}{y}^{\mathrm{2}} \:=\:? \\ $$
Answered by Rasheed.Sindhi last updated on 30/Jul/21
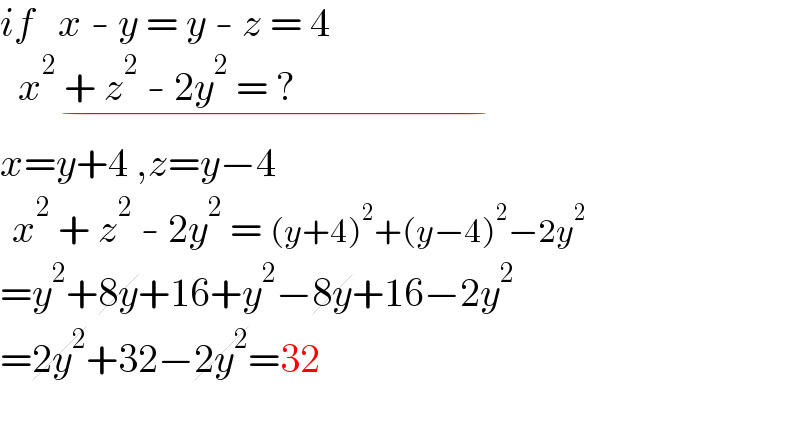
$${if}\:\:\:{x}\:-\:{y}\:=\:{y}\:-\:{z}\:=\:\mathrm{4} \\ $$$$\underset{−} {\:\:\:{x}^{\mathrm{2}} \:+\:{z}^{\mathrm{2}} \:-\:\mathrm{2}{y}^{\mathrm{2}} \:=\:?\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:} \\ $$$${x}={y}+\mathrm{4}\:,{z}={y}−\mathrm{4} \\ $$$$\:\:{x}^{\mathrm{2}} \:+\:{z}^{\mathrm{2}} \:-\:\mathrm{2}{y}^{\mathrm{2}} \:=\:\left({y}+\mathrm{4}\right)^{\mathrm{2}} +\left({y}−\mathrm{4}\right)^{\mathrm{2}} −\mathrm{2}{y}^{\mathrm{2}} \\ $$$$={y}^{\mathrm{2}} +\cancel{\mathrm{8}{y}}+\mathrm{16}+{y}^{\mathrm{2}} −\cancel{\mathrm{8}{y}}+\mathrm{16}−\mathrm{2}{y}^{\mathrm{2}} \\ $$$$=\cancel{\mathrm{2}{y}^{\mathrm{2}} }+\mathrm{32}−\cancel{\mathrm{2}{y}^{\mathrm{2}} }=\mathrm{32} \\ $$$$ \\ $$
Commented by mathdanisur last updated on 30/Jul/21

$${Thank}\:{You}\:{Ser} \\ $$
