Menu Close

if-x-y-z-0-then-2-x-y-z-2-2-x-2-y-2-z-

Tinku Tara 0 Comments
Pin




Question Number 157436 by MathSh last updated on 23/Oct/21
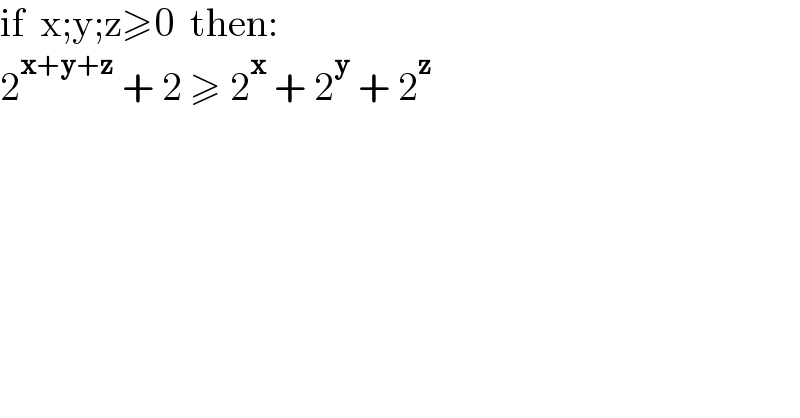
if x;y;z≥0 then: 2^(x+y+z) + 2 ≥ 2^x + 2^y + 2^z
$$\mathrm{if}\:\:\mathrm{x};\mathrm{y};\mathrm{z}\geqslant\mathrm{0}\:\:\mathrm{then}: \\ $$$$\mathrm{2}^{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}+\boldsymbol{\mathrm{z}}} \:+\:\mathrm{2}\:\geqslant\:\mathrm{2}^{\boldsymbol{\mathrm{x}}} \:+\:\mathrm{2}^{\boldsymbol{\mathrm{y}}} \:+\:\mathrm{2}^{\boldsymbol{\mathrm{z}}} \\ $$$$ \\ $$
Answered by Jamshidbek last updated on 23/Oct/21
Solution. 2^x =a≥1 2^y =b≥1 2^z =c≥1 abc+2≥a+b+c ⇒ abc−a+2−(b+c)≥0 abc−bc−a+1+bc−b+1−c≥0 bc(a−1)−(a−1)+b(c−1)−(c−1)≥0 (a−1)(bc−1)+(b−1)(c−1)≥0
$$\mathrm{Solution}. \\ $$$$\mathrm{2}^{\mathrm{x}} =\mathrm{a}\geqslant\mathrm{1}\:\mathrm{2}^{\mathrm{y}} =\mathrm{b}\geqslant\mathrm{1}\:\:\mathrm{2}^{\mathrm{z}} =\mathrm{c}\geqslant\mathrm{1} \\ $$$$\mathrm{abc}+\mathrm{2}\geqslant\mathrm{a}+\mathrm{b}+\mathrm{c}\:\Rightarrow\:\mathrm{abc}−\mathrm{a}+\mathrm{2}−\left(\mathrm{b}+\mathrm{c}\right)\geqslant\mathrm{0} \\ $$$$\mathrm{abc}−\mathrm{bc}−\mathrm{a}+\mathrm{1}+\mathrm{bc}−\mathrm{b}+\mathrm{1}−\mathrm{c}\geqslant\mathrm{0} \\ $$$$\mathrm{bc}\left(\mathrm{a}−\mathrm{1}\right)−\left(\mathrm{a}−\mathrm{1}\right)+\mathrm{b}\left(\mathrm{c}−\mathrm{1}\right)−\left(\mathrm{c}−\mathrm{1}\right)\geqslant\mathrm{0} \\ $$$$\left(\mathrm{a}−\mathrm{1}\right)\left(\mathrm{bc}−\mathrm{1}\right)+\left(\mathrm{b}−\mathrm{1}\right)\left(\mathrm{c}−\mathrm{1}\right)\geqslant\mathrm{0} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *