Question Number 147488 by mathdanisur last updated on 21/Jul/21
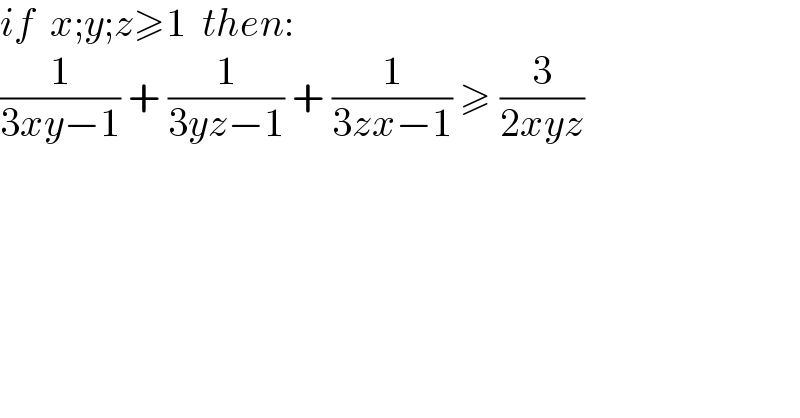
$${if}\:\:{x};{y};{z}\geqslant\mathrm{1}\:\:{then}: \\ $$$$\frac{\mathrm{1}}{\mathrm{3}{xy}−\mathrm{1}}\:+\:\frac{\mathrm{1}}{\mathrm{3}{yz}−\mathrm{1}}\:+\:\frac{\mathrm{1}}{\mathrm{3}{zx}−\mathrm{1}}\:\geqslant\:\frac{\mathrm{3}}{\mathrm{2}{xyz}} \\ $$
Answered by mindispower last updated on 21/Jul/21
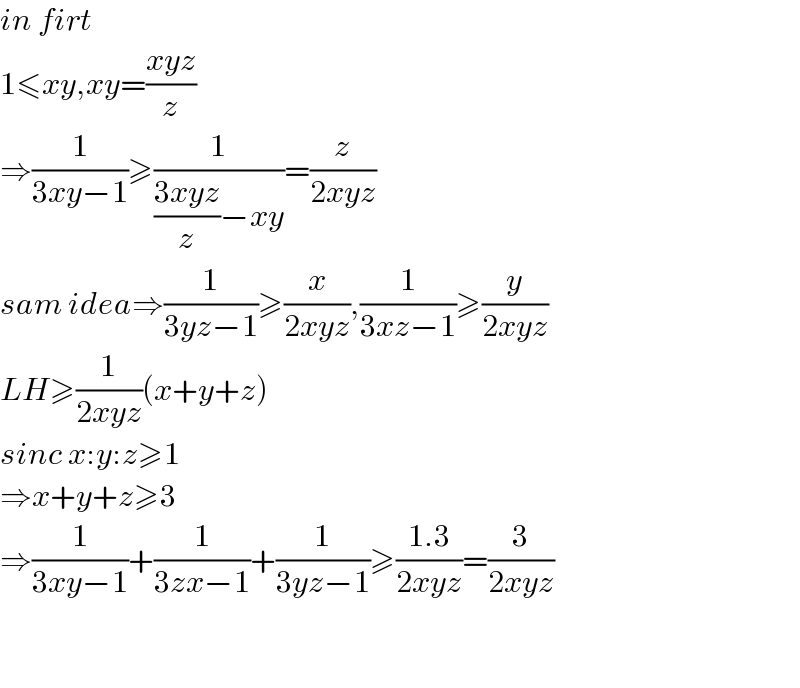
$${in}\:{firt} \\ $$$$\mathrm{1}\leqslant{xy},{xy}=\frac{{xyz}}{{z}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{3}{xy}−\mathrm{1}}\geqslant\frac{\mathrm{1}}{\frac{\mathrm{3}{xyz}}{{z}}−{xy}}=\frac{{z}}{\mathrm{2}{xyz}} \\ $$$${sam}\:{idea}\Rightarrow\frac{\mathrm{1}}{\mathrm{3}{yz}−\mathrm{1}}\geqslant\frac{{x}}{\mathrm{2}{xyz}},\frac{\mathrm{1}}{\mathrm{3}{xz}−\mathrm{1}}\geqslant\frac{{y}}{\mathrm{2}{xyz}} \\ $$$${LH}\geqslant\frac{\mathrm{1}}{\mathrm{2}{xyz}}\left({x}+{y}+{z}\right) \\ $$$${sinc}\:{x}:{y}:{z}\geqslant\mathrm{1} \\ $$$$\Rightarrow{x}+{y}+{z}\geqslant\mathrm{3} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{3}{xy}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{3}{zx}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{3}{yz}−\mathrm{1}}\geqslant\frac{\mathrm{1}.\mathrm{3}}{\mathrm{2}{xyz}}=\frac{\mathrm{3}}{\mathrm{2}{xyz}} \\ $$$$ \\ $$$$ \\ $$
Commented by mathdanisur last updated on 21/Jul/21
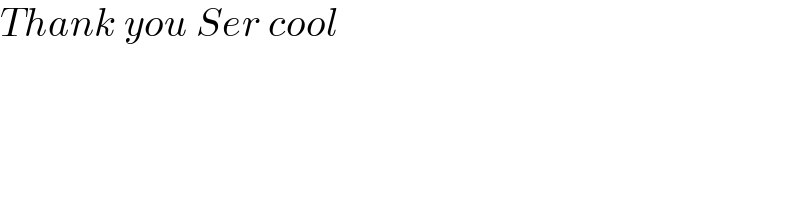
$${Thank}\:{you}\:{Ser}\:{cool} \\ $$
