if-x-y-z-1-x-2-y-2-z-2-2-x-3-y-3-z-3-3-find-x-4-y-4-z-4-

Question Number 52592 by tanmay.chaudhury50@gmail.com last updated on 10/Jan/19

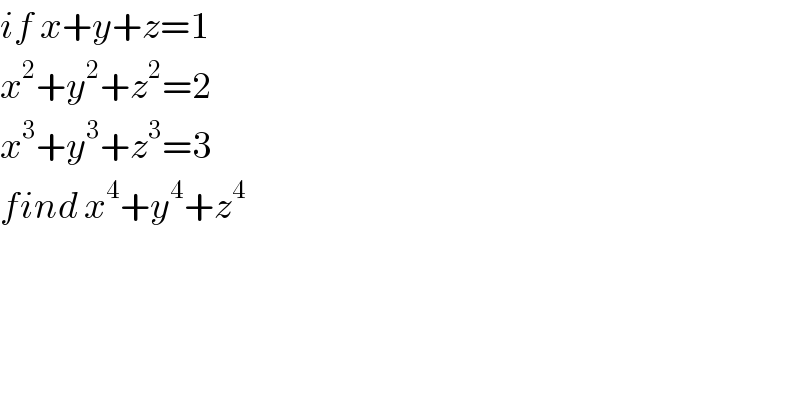
i f x + y + z = 1

x^{2} + y^{2} + z^{2} = 2

x^{3} + y^{3} + z^{3} = 3

f i n d x^{4} + y^{4} + z^{4}

Answered by math1967 last updated on 10/Jan/19

x + y + z = 1

\Rightarrow 2 (x y + y z + z x) = 1 - 2 = - 1

∴ (x y + y z + z x) = - \frac{1}{2}

x^{2} y^{2} + y^{2} z^{2} + z^{2} x^{2} + 2 x y z (x + y + z) = \frac{1}{4}

x^{2} y^{2} + y^{2} z^{2} + z^{2} x^{2} = \frac{1}{4} - \frac{1}{3} = - \frac{1}{12} ★

x^{3} + y^{3} + z^{3} - 3 x y z + 3 x y z = 3 ★

(x + y + z) (x^{2} + y^{2} + z^{2} - x y - y z - z x) + 3 x y z = 3

3 x y z = 3 - \frac{5}{2} = \frac{1}{2} \Rightarrow x y z = \frac{1}{6}

{(x^{2} + y^{2} + z^{2})}^{2} = 4

x^{4} + y^{4} + z^{4} + 2 (x^{2} y^{2} + y^{2} z^{2} + z^{2} x^{2}) = 4

x^{4} + y^{4} + z^{4} = 4 + \frac{1}{6} = 4 \frac{1}{6} a n s

Commented by tanmay.chaudhury50@gmail.com last updated on 10/Jan/19

b a h d a r u n e x c e l l e n t \dots

Commented by math1967 last updated on 10/Jan/19

d h a n y a b a d