Question Number 147944 by mathdanisur last updated on 24/Jul/21
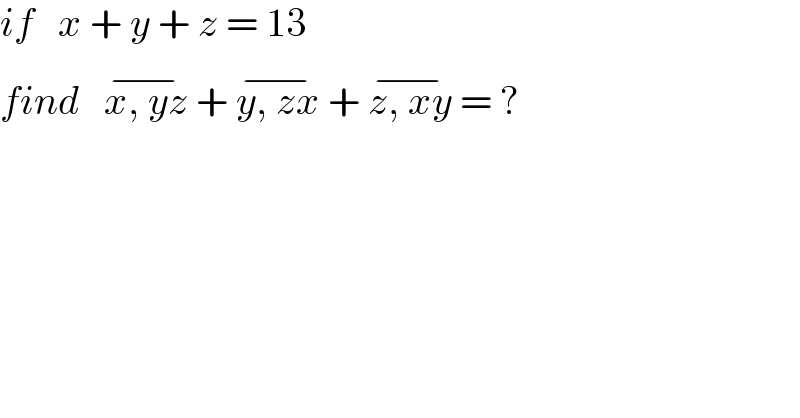
$${if}\:\:\:{x}\:+\:{y}\:+\:{z}\:=\:\mathrm{13} \\ $$$${find}\:\:\:\overline {{x},\:{yz}}\:+\:\overline {{y},\:{zx}}\:+\:\overline {{z},\:{xy}}\:=\:? \\ $$
Answered by Rasheed.Sindhi last updated on 25/Jul/21

$$\:{x}+{y}+{z}=\mathrm{13}\:;\:\:\overline {{x},\:{yz}}\:+\:\overline {{y},\:{zx}}\:+\:\overline {{z},\:{xy}}=? \\ $$$$\smile\frown\smile\frown\smile\frown\smile\frown\smile\frown\smile\frown\smile\frown\smile \\ $$$$\left({x}+\frac{{y}}{\mathrm{10}}+\frac{{z}}{\mathrm{100}}\right)+\left({y}+\frac{{z}}{\mathrm{10}}+\frac{{x}}{\mathrm{100}}\right)+\left({z}+\frac{{x}}{\mathrm{10}}+\frac{{y}}{\mathrm{100}}\right) \\ $$$$=\frac{\mathrm{100}{x}+\mathrm{10}{y}+{z}}{\mathrm{100}}+\frac{\mathrm{100}{y}+\mathrm{10}{z}+{x}}{\mathrm{100}}+\frac{\mathrm{100}{z}+\mathrm{10}{x}+{y}}{\mathrm{100}} \\ $$$$=\frac{\mathrm{111}{x}+\mathrm{111}{y}+\mathrm{111}{z}}{\mathrm{100}} \\ $$$${z}=\mathrm{13}−{x}−{y}\:: \\ $$$$=\frac{\mathrm{111}{x}+\mathrm{111}{y}+\mathrm{111}\left(\mathrm{13}−{x}−{y}\right)}{\mathrm{100}} \\ $$$$=\frac{\cancel{\mathrm{111}{x}}+\cancel{\mathrm{111}{y}}+\mathrm{1443}−\cancel{\mathrm{111}{x}}−\cancel{\mathrm{111}{y}}}{\mathrm{100}} \\ $$$$=\mathrm{1443}/\mathrm{100}=\mathrm{14}.\mathrm{43} \\ $$
Commented by mathdanisur last updated on 24/Jul/21

$${Thank}\:{you}\:{Ser} \\ $$
