Question Number 176847 by Ar Brandon last updated on 27/Sep/22
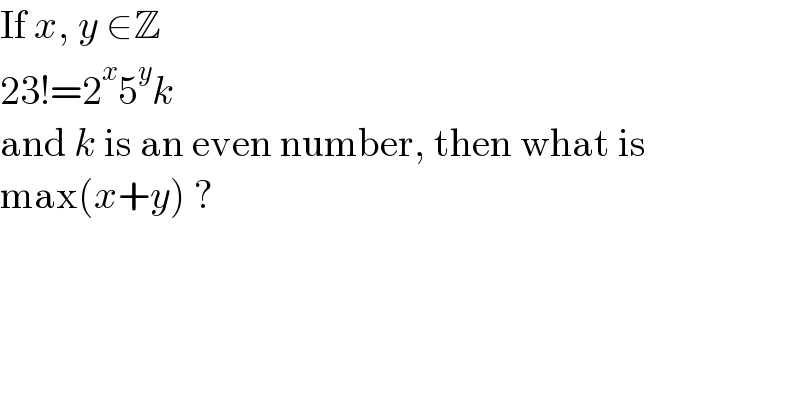
$$\mathrm{If}\:{x},\:{y}\:\in\mathbb{Z} \\ $$$$\mathrm{23}!=\mathrm{2}^{{x}} \mathrm{5}^{{y}} {k} \\ $$$$\mathrm{and}\:{k}\:\mathrm{is}\:\mathrm{an}\:\mathrm{even}\:\mathrm{number},\:\mathrm{then}\:\mathrm{what}\:\mathrm{is}\: \\ $$$$\mathrm{max}\left({x}+{y}\right)\:? \\ $$
Answered by BaliramKumar last updated on 27/Sep/22
![determinant ((2,(23)),(2,(11)),(2,5),(2,2),(2,1),(,0)) & determinant ((5,(23)),(5,4),(,0)) determinant ((),()) x = 11+5+2+1+0 = 19 y = 4+0 = 4 23! = 2^(19) ×5^4 ×x [where ′x′ will be odd] 23! = 2^(18) ×5^4 ×(2x) 23! = 2^(18) ×5^4 ×k [2x = k] max(x+y) = 18+4 = determinant (((22)))](https://www.tinkutara.com/question/Q176883.png)
$$ \\ $$$$\begin{array}{|c|c|c|c|c|c|}{\mathrm{2}}&\hline{\mathrm{23}}\\{\mathrm{2}}&\hline{\mathrm{11}}\\{\mathrm{2}}&\hline{\mathrm{5}}\\{\mathrm{2}}&\hline{\mathrm{2}}\\{\mathrm{2}}&\hline{\mathrm{1}}\\{}&\hline{\mathrm{0}}\\\hline\end{array}\:\:\:\:\:\:\&\:\:\:\:\:\:\begin{array}{|c|c|c|}{\mathrm{5}}&\hline{\mathrm{23}}\\{\mathrm{5}}&\hline{\mathrm{4}}\\{}&\hline{\mathrm{0}}\\\hline\end{array}\begin{array}{|c|c|}\\\\\hline\end{array} \\ $$$${x}\:=\:\mathrm{11}+\mathrm{5}+\mathrm{2}+\mathrm{1}+\mathrm{0}\:=\:\mathrm{19} \\ $$$${y}\:=\:\mathrm{4}+\mathrm{0}\:=\:\mathrm{4} \\ $$$$\mathrm{23}!\:=\:\mathrm{2}^{\mathrm{19}} ×\mathrm{5}^{\mathrm{4}} ×{x}\:\:\:\:\:\:\:\:\:\:\:\:\:\left[{where}\:'{x}'\:{will}\:{be}\:{odd}\right] \\ $$$$\mathrm{23}!\:=\:\mathrm{2}^{\mathrm{18}} ×\mathrm{5}^{\mathrm{4}} ×\left(\mathrm{2}{x}\right) \\ $$$$\mathrm{23}!\:=\:\mathrm{2}^{\mathrm{18}} ×\mathrm{5}^{\mathrm{4}} ×{k}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\mathrm{2}{x}\:=\:{k}\right] \\ $$$${max}\left({x}+{y}\right)\:=\:\mathrm{18}+\mathrm{4}\:=\:\begin{array}{|c|}{\mathrm{22}}\\\hline\end{array} \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 28/Sep/22
Thanks
Answered by mr W last updated on 27/Sep/22
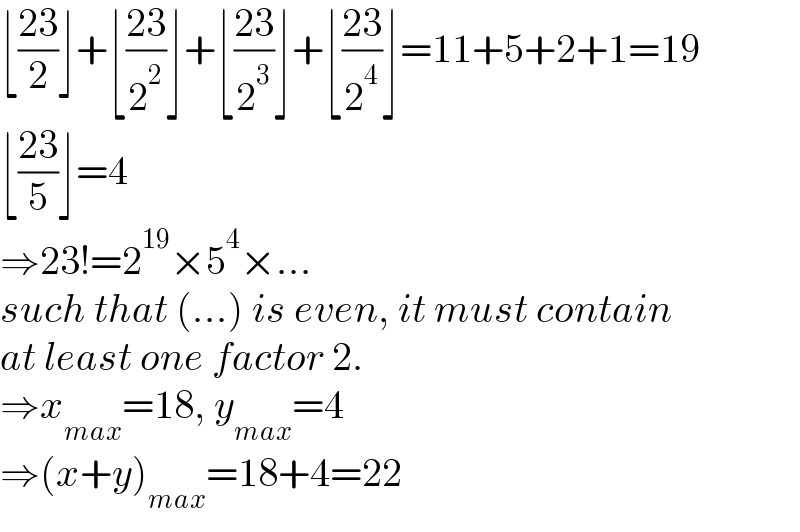
$$\lfloor\frac{\mathrm{23}}{\mathrm{2}}\rfloor+\lfloor\frac{\mathrm{23}}{\mathrm{2}^{\mathrm{2}} }\rfloor+\lfloor\frac{\mathrm{23}}{\mathrm{2}^{\mathrm{3}} }\rfloor+\lfloor\frac{\mathrm{23}}{\mathrm{2}^{\mathrm{4}} }\rfloor=\mathrm{11}+\mathrm{5}+\mathrm{2}+\mathrm{1}=\mathrm{19} \\ $$$$\lfloor\frac{\mathrm{23}}{\mathrm{5}}\rfloor=\mathrm{4} \\ $$$$\Rightarrow\mathrm{23}!=\mathrm{2}^{\mathrm{19}} ×\mathrm{5}^{\mathrm{4}} ×… \\ $$$${such}\:{that}\:\left(…\right)\:{is}\:{even},\:{it}\:{must}\:{contain} \\ $$$${at}\:{least}\:{one}\:{factor}\:\mathrm{2}. \\ $$$$\Rightarrow{x}_{{max}} =\mathrm{18},\:{y}_{{max}} =\mathrm{4} \\ $$$$\Rightarrow\left({x}+{y}\right)_{{max}} =\mathrm{18}+\mathrm{4}=\mathrm{22} \\ $$
Commented by Ar Brandon last updated on 27/Sep/22
Thank you ��
Answered by Rasheed.Sindhi last updated on 27/Sep/22

$$\mathrm{2}\:\mathrm{4}\:\mathrm{6}\:\mathrm{8}\:\mathrm{10}\:\mathrm{12}\:\mathrm{14}\:\mathrm{16}\:\mathrm{18}\:\mathrm{20}\:\mathrm{22}……\mathrm{11} \\ $$$$\mathrm{4}\:\mathrm{8}\:\mathrm{12}\:\mathrm{16}\:\mathrm{20}……….\mathrm{5} \\ $$$$\mathrm{8}\:\mathrm{16}………………\mathrm{2} \\ $$$$\mathrm{16}…………………\mathrm{1} \\ $$$$\mathrm{11}+\mathrm{5}+\mathrm{2}+\mathrm{1}=\mathrm{19}\:\mathrm{2}'{s} \\ $$$${k}\:{ieven}\:{maximum}\:{x}\:{is}\:\mathrm{18} \\ $$$$\mathrm{5}\:\mathrm{10}\:\mathrm{15}\:\mathrm{20}………..\mathrm{4}\: \\ $$$${maximum}\:{y}\:\:\mathrm{4} \\ $$$${max}\left({x}+{y}\right)=\mathrm{18}+\mathrm{4}=\mathrm{22} \\ $$
Commented by Ar Brandon last updated on 27/Sep/22
Thanks ��
