Question Number 149585 by mathdanisur last updated on 06/Aug/21
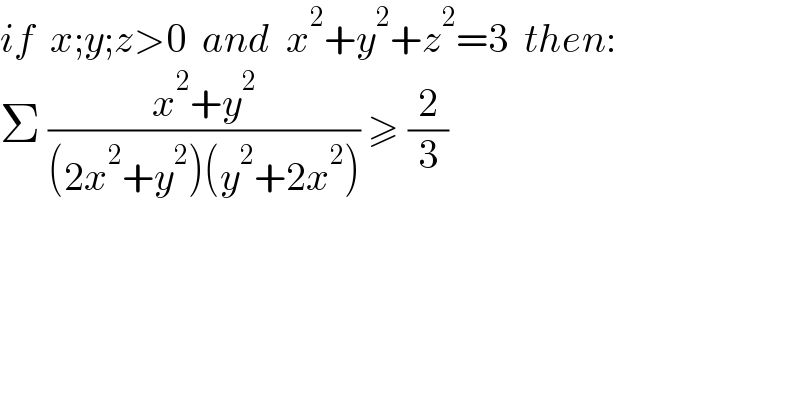
$${if}\:\:{x};{y};{z}>\mathrm{0}\:\:{and}\:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} =\mathrm{3}\:\:{then}: \\ $$$$\Sigma\:\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\left(\mathrm{2}{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\left({y}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{2}} \right)}\:\geqslant\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Answered by dumitrel last updated on 06/Aug/21
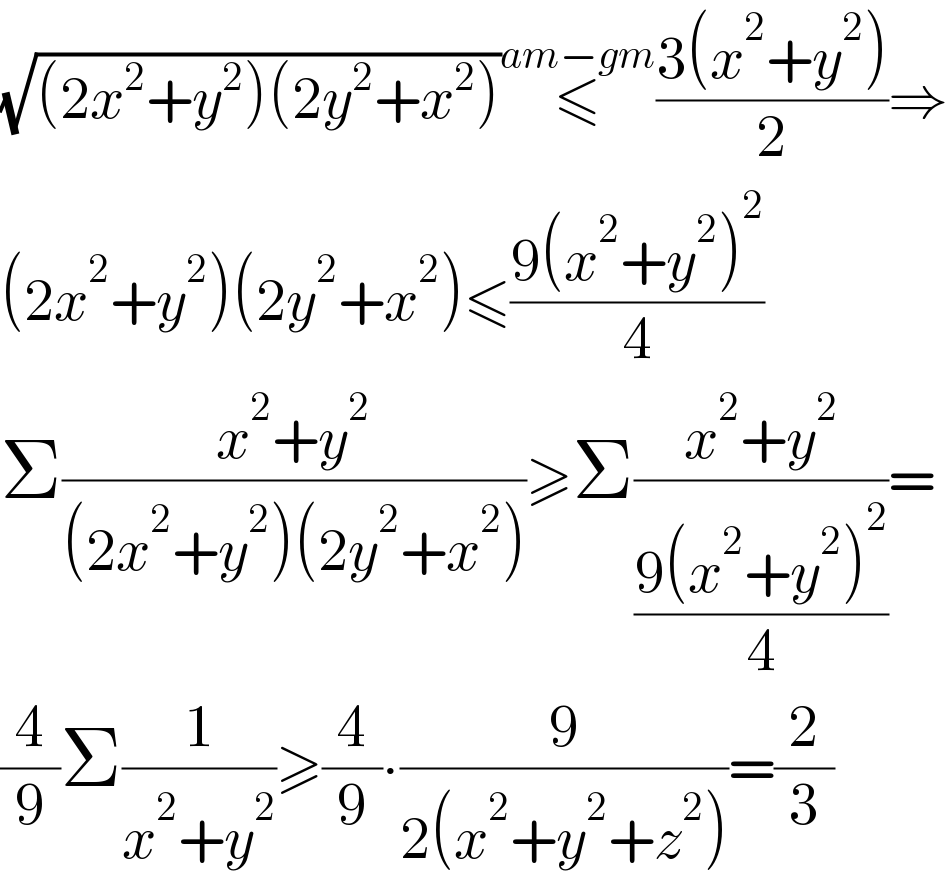
$$\sqrt{\left(\mathrm{2}{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\left(\mathrm{2}{y}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)}\overset{{am}−{gm}} {\leqslant}\frac{\mathrm{3}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)}{\mathrm{2}}\Rightarrow \\ $$$$\left(\mathrm{2}{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\left(\mathrm{2}{y}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)\leqslant\frac{\mathrm{9}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Sigma\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\left(\mathrm{2}{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\left(\mathrm{2}{y}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)}\geqslant\Sigma\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\frac{\mathrm{9}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{4}}}= \\ $$$$\frac{\mathrm{4}}{\mathrm{9}}\Sigma\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\geqslant\frac{\mathrm{4}}{\mathrm{9}}\centerdot\frac{\mathrm{9}}{\mathrm{2}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by mathdanisur last updated on 06/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\boldsymbol{\mathrm{Ser}},\:\mathrm{cool} \\ $$
