Question Number 144600 by mathdanisur last updated on 26/Jun/21
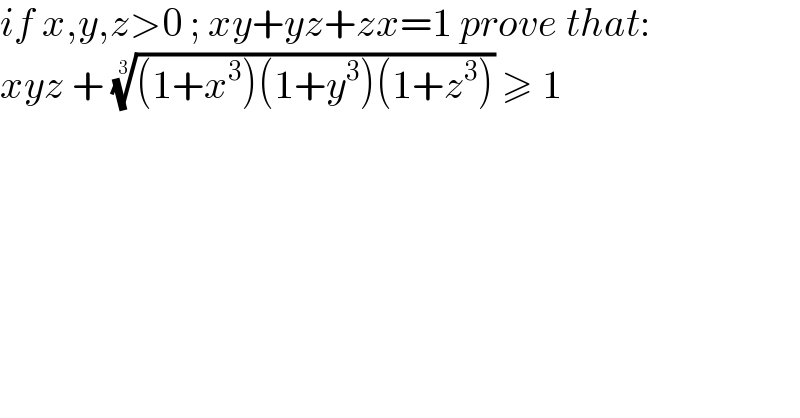
$${if}\:{x},{y},{z}>\mathrm{0}\:;\:{xy}+{yz}+{zx}=\mathrm{1}\:{prove}\:{that}: \\ $$$${xyz}\:+\:\sqrt[{\mathrm{3}}]{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)\left(\mathrm{1}+{y}^{\mathrm{3}} \right)\left(\mathrm{1}+{z}^{\mathrm{3}} \right)}\:\geqslant\:\mathrm{1} \\ $$
Answered by mindispower last updated on 27/Jun/21

$${x},{y},{z}>\mathrm{0} \\ $$$${or}\:{only}\:{z}>\mathrm{0} \\ $$
Commented by mathdanisur last updated on 27/Jun/21

$${Thanks}\:{Sir},\:{how}… \\ $$
