Question Number 149891 by mathdanisur last updated on 08/Aug/21
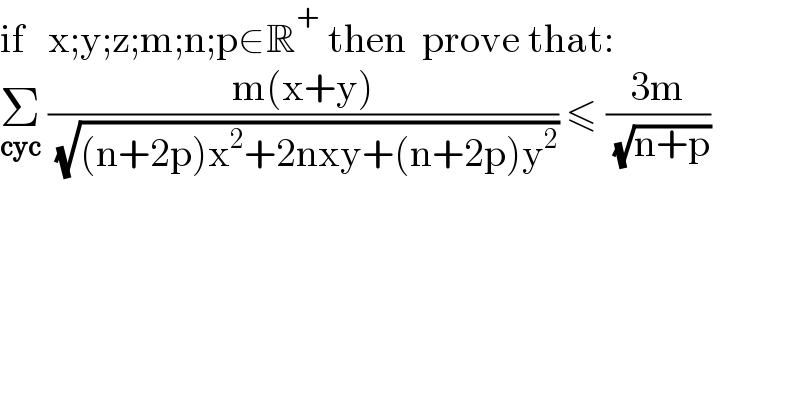
$$\mathrm{if}\:\:\:\mathrm{x};\mathrm{y};\mathrm{z};\mathrm{m};\mathrm{n};\mathrm{p}\in\mathbb{R}^{+} \:\mathrm{then}\:\:\mathrm{prove}\:\mathrm{that}: \\ $$$$\underset{\boldsymbol{\mathrm{cyc}}} {\sum}\:\frac{\mathrm{m}\left(\mathrm{x}+\mathrm{y}\right)}{\:\sqrt{\left(\mathrm{n}+\mathrm{2p}\right)\mathrm{x}^{\mathrm{2}} +\mathrm{2nxy}+\left(\mathrm{n}+\mathrm{2p}\right)\mathrm{y}^{\mathrm{2}} }}\:\leqslant\:\frac{\mathrm{3m}}{\:\sqrt{\mathrm{n}+\mathrm{p}}} \\ $$
Answered by dumitrel last updated on 08/Aug/21
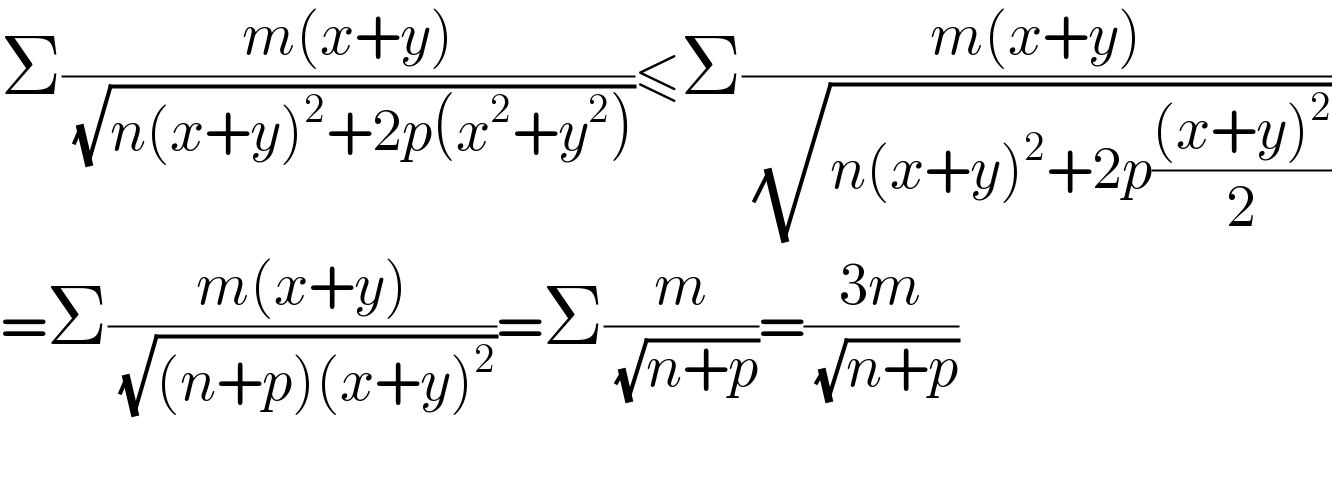
$$\Sigma\frac{{m}\left({x}+{y}\right)}{\:\sqrt{{n}\left({x}+{y}\right)^{\mathrm{2}} +\mathrm{2}{p}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)}}\leqslant\Sigma\frac{{m}\left({x}+{y}\right)}{\:\sqrt{{n}\left({x}+{y}\right)^{\mathrm{2}} +\mathrm{2}{p}\frac{\left({x}+{y}\right)^{\mathrm{2}} }{\mathrm{2}}}} \\ $$$$=\Sigma\frac{{m}\left({x}+{y}\right)}{\:\sqrt{\left({n}+{p}\right)\left({x}+{y}\right)^{\mathrm{2}} }}=\Sigma\frac{{m}}{\:\sqrt{{n}+{p}}}=\frac{\mathrm{3}{m}}{\:\sqrt{{n}+{p}}} \\ $$$$ \\ $$
Commented by mathdanisur last updated on 08/Aug/21
$$\mathrm{Cool}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{thank}\:\mathrm{you} \\ $$
