Question Number 85854 by jagoll last updated on 25/Mar/20
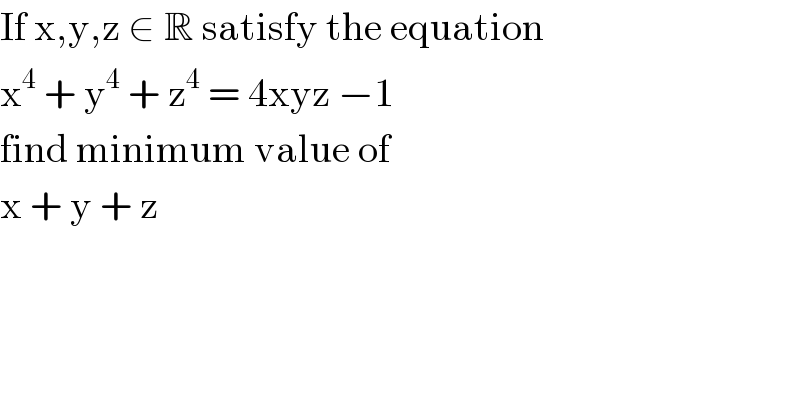
$$\mathrm{If}\:\mathrm{x},\mathrm{y},\mathrm{z}\:\in\:\mathbb{R}\:\mathrm{satisfy}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{x}^{\mathrm{4}} \:+\:\mathrm{y}^{\mathrm{4}} \:+\:\mathrm{z}^{\mathrm{4}} \:=\:\mathrm{4xyz}\:−\mathrm{1}\: \\ $$$$\mathrm{find}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of} \\ $$$$\mathrm{x}\:+\:\mathrm{y}\:+\:\mathrm{z}\: \\ $$
Commented by mr W last updated on 25/Mar/20

$${seems}\:{to}\:{be}\:\mathrm{3} \\ $$
Commented by mr W last updated on 25/Mar/20
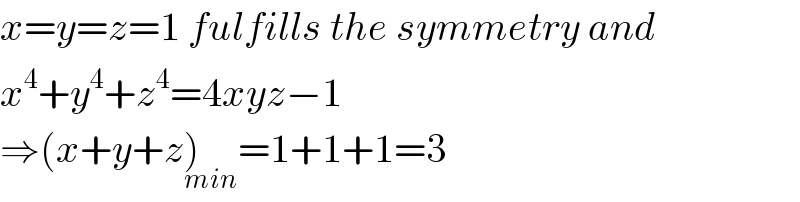
$${x}={y}={z}=\mathrm{1}\:{fulfills}\:{the}\:{symmetry}\:{and} \\ $$$${x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} =\mathrm{4}{xyz}−\mathrm{1} \\ $$$$\Rightarrow\left({x}+{y}+{z}\underset{{min}} {\right)}=\mathrm{1}+\mathrm{1}+\mathrm{1}=\mathrm{3} \\ $$
