Question Number 156824 by Tawa11 last updated on 15/Oct/21
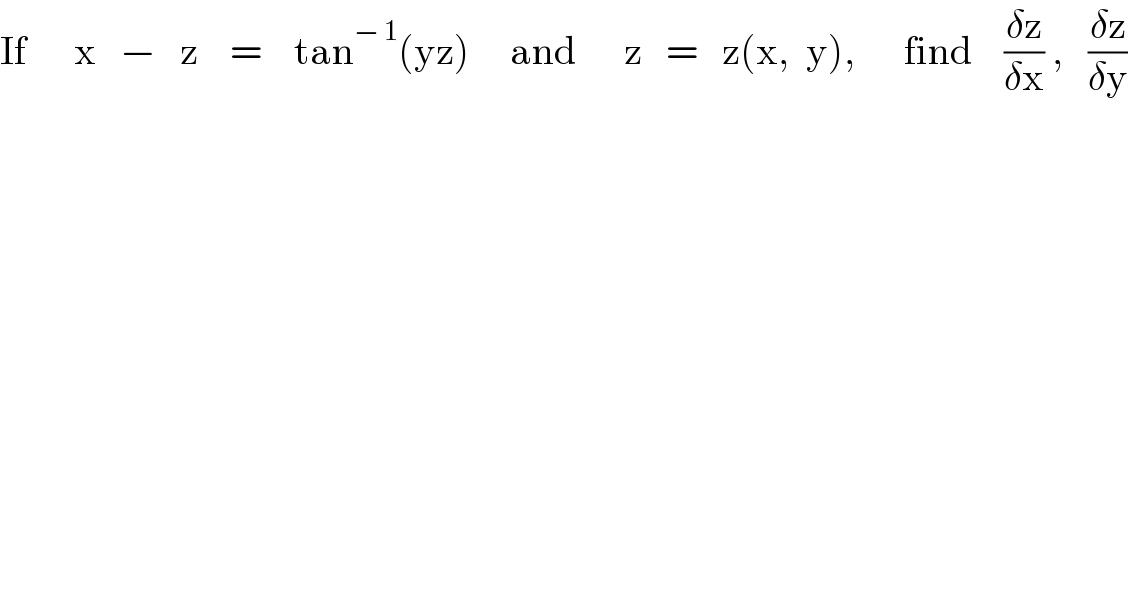
$$\mathrm{If}\:\:\:\:\:\:\mathrm{x}\:\:\:−\:\:\:\mathrm{z}\:\:\:\:=\:\:\:\:\mathrm{tan}^{−\:\mathrm{1}} \left(\mathrm{yz}\right)\:\:\:\:\:\mathrm{and}\:\:\:\:\:\:\mathrm{z}\:\:\:=\:\:\:\mathrm{z}\left(\mathrm{x},\:\:\mathrm{y}\right),\:\:\:\:\:\:\mathrm{find}\:\:\:\:\frac{\delta\mathrm{z}}{\delta\mathrm{x}}\:,\:\:\:\frac{\delta\mathrm{z}}{\delta\mathrm{y}} \\ $$
Answered by mr W last updated on 16/Oct/21
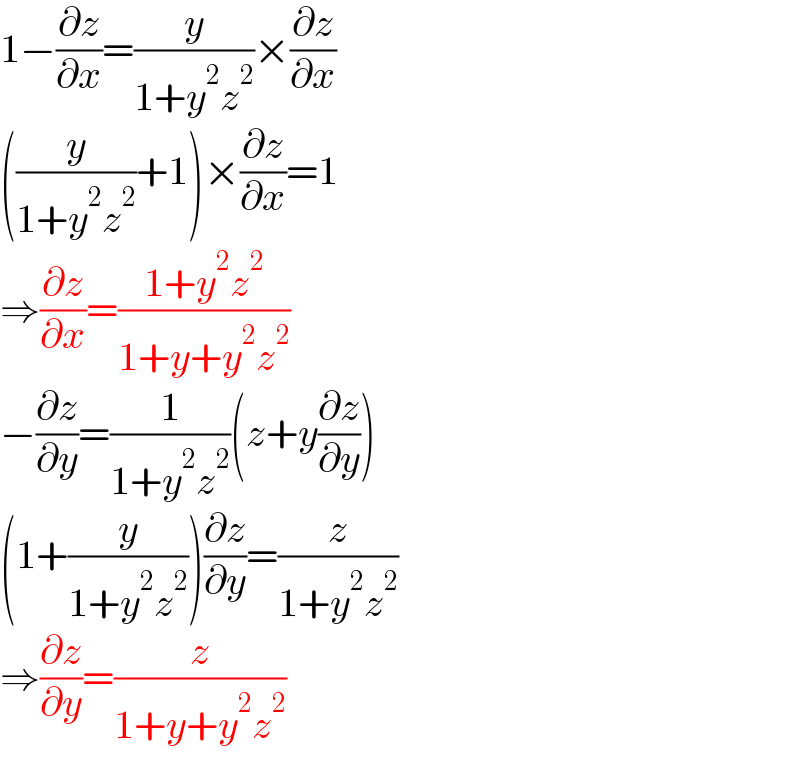
$$\mathrm{1}−\frac{\partial{z}}{\partial{x}}=\frac{{y}}{\mathrm{1}+{y}^{\mathrm{2}} {z}^{\mathrm{2}} }×\frac{\partial{z}}{\partial{x}} \\ $$$$\left(\frac{{y}}{\mathrm{1}+{y}^{\mathrm{2}} {z}^{\mathrm{2}} }+\mathrm{1}\right)×\frac{\partial{z}}{\partial{x}}=\mathrm{1} \\ $$$$\Rightarrow\frac{\partial{z}}{\partial{x}}=\frac{\mathrm{1}+{y}^{\mathrm{2}} {z}^{\mathrm{2}} }{\mathrm{1}+{y}+{y}^{\mathrm{2}} {z}^{\mathrm{2}} } \\ $$$$−\frac{\partial{z}}{\partial{y}}=\frac{\mathrm{1}}{\mathrm{1}+{y}^{\mathrm{2}} {z}^{\mathrm{2}} }\left({z}+{y}\frac{\partial{z}}{\partial{y}}\right) \\ $$$$\left(\mathrm{1}+\frac{{y}}{\mathrm{1}+{y}^{\mathrm{2}} {z}^{\mathrm{2}} }\right)\frac{\partial{z}}{\partial{y}}=\frac{{z}}{\mathrm{1}+{y}^{\mathrm{2}} {z}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{\partial{z}}{\partial{y}}=\frac{{z}}{\mathrm{1}+{y}+{y}^{\mathrm{2}} {z}^{\mathrm{2}} } \\ $$
Commented by Tawa11 last updated on 16/Oct/21
$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
